题目内容
13.阅读下列文字:对于一个图形,通过不同的方法计算图形的面积,可以得到一个数学等式,例如:由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.请解答下列问题:(1)写出图2中所表示的数学等式(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.;
(2)利用(1)中所得到的结论,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片,长为b和宽为a的长方形纸片,利用所给的纸片拼出一个几何图形,使得计算它的面积能得到数学公式:2a2+3ab+b2=(2a+b)(a+b).
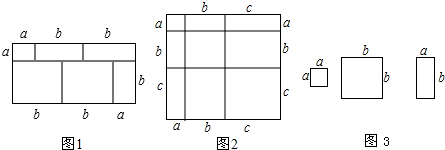
分析 (1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.
(2)根据利用(1)中所得到的结论,将a+b+c=11,ab+bc+ac=38作为整式代入即可求出.
(3)找规律,根据公式画出图形,拼成一个长方形,使它满足所给的条件
解答 解:(1)根据题意,大矩形的面积为:(a+b+c)(a+b+c)=(a+b+c)2,
各小矩形部分的面积之和=a2+2ab+b2+2bc+2ac+c2,
∴(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(2)a2+b2+c2=(a+b+c)2-2(ab+ac+bc)=112-2×38=45.
(3)如图所示:
点评 本题考查了完全平方公式的几何背景,根据矩形的面积公式分整体与部分两种思路表示出面积,然后再根据同一个图形的面积相等即可解答.

练习册系列答案
相关题目
12.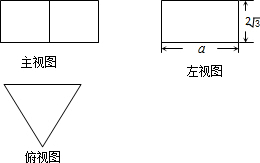 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | 2+$\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
4.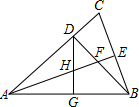 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )| A. | AH=2DF | B. | AF=2HE | C. | AF=2CE | D. | DH=DF |
1.计算(-x3)2的结果是( )
| A. | -x5 | B. | x5 | C. | -x6 | D. | x6 |
8.下列语句中,是命题的是( )
| A. | 过直线l外一点作l的平行线 | B. | 美丽的天空 | ||
| C. | 你的作业做完了吗? | D. | 对顶角相等 |
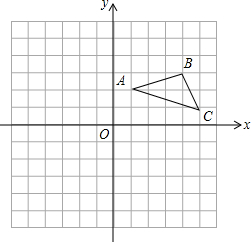 在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题:
在平面直角坐标系中,△ABC的位置如图,网格中小正方形的边长为1,请解答下列问题: