题目内容
17.双曲线y=$\frac{k}{x}$上三点A、B、C,三点的横坐标分别为-1、-6、$\frac{2}{3}$,且AB⊥AC,则实数k的值为2.-2.分析 分别作AM∥y轴,CM⊥y轴,AM、CM相交于M,过B作BN⊥AM于N,分别表示出点A、B、C的纵坐标,表示出AN、BN、AM、CM的长度,然后利用三角形相似对应边成比例得出k2=4,然后即可求出k的值.
解答 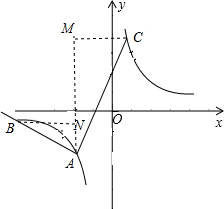 解:∵双曲线y=$\frac{k}{x}$上三点A、B、C,三点的横坐标分别为-1、-6、$\frac{2}{3}$,
解:∵双曲线y=$\frac{k}{x}$上三点A、B、C,三点的横坐标分别为-1、-6、$\frac{2}{3}$,
∴A(-1,-k),B(-6,-$\frac{k}{6}$),C($\frac{2}{3}$,$\frac{3}{2}$k),
作AM∥y轴,CM⊥y轴,AM、CM相交于M,过B作BN⊥AM于N,
∴AN=|k-$\frac{k}{6}$|=$\frac{5}{6}$|k|,BN=6-1=5,AM=|k|+|$\frac{3}{2}$k|=$\frac{5}{2}$|k|,CM=1+$\frac{2}{3}$=$\frac{5}{3}$,
∵AB⊥AC,
∴∠BAN+∠MAC=90°.
∵∠ABN+∠BAN=90°,
∴∠ABN=∠MAC,
∵∠ANB=∠CMA=90°,
∴△ANB∽△CMA,
∴$\frac{BN}{AM}$=$\frac{AN}{CM}$,即$\frac{5}{\frac{5}{2}|k|}$=$\frac{\frac{5}{6}|k|}{\frac{5}{3}}$,
∴k2=4,
∴k=±2.
故答案为2,-2.
点评 本题考查了反比例函数图象上点的特征,主要是根据反比例函数的解析式表示出AN、BN、AM、CM的长度,进而根据三角形相似对应边成比例求出k的值,作出辅助线关键相似三角形是本题的关键.

练习册系列答案
相关题目
8.$\sqrt{(3.1-\sqrt{10})^{2}}$的值等于( )
| A. | $\sqrt{10}$-3.1 | B. | 3.1±$\sqrt{10}$ | C. | 3.1-$\sqrt{10}$ | D. | ±(3.1-$\sqrt{10}$) |
12.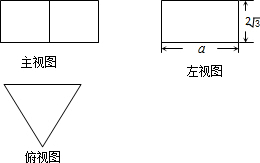 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | 2+$\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
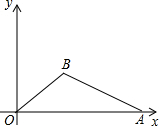 如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=$\frac{3}{5}$.
如图,在直角坐标平面中,O为原点,点A的坐标为(20,0),点B在第一象限内,BO=10,sin∠BOA=$\frac{3}{5}$.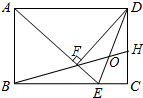 矩形ABCD中,AD=$\sqrt{2}$AB,AE平分∠BAD,DF⊥AE于F,BF交DE、CD于O、H,下列结论:①∠DEA=3∠EDC;②BF=FH;③OE=OD;④BC-CH=2EF,其中结论正确的个数有( )
矩形ABCD中,AD=$\sqrt{2}$AB,AE平分∠BAD,DF⊥AE于F,BF交DE、CD于O、H,下列结论:①∠DEA=3∠EDC;②BF=FH;③OE=OD;④BC-CH=2EF,其中结论正确的个数有( )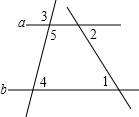 已知,如图所示,∠3=110°,∠4=70°,∠1=46°,求∠2的度数.
已知,如图所示,∠3=110°,∠4=70°,∠1=46°,求∠2的度数.