题目内容
12.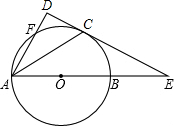 如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.
如图,已知AB是⊙O的直径,直线CE与⊙O相切于点C,交AB的延长线交于点E.作AD⊥CE,垂足为D,连接AC.求证:AC平分∠DAB.
分析 连结OC,如图,根据切线的性质得OC⊥CE,加上AD⊥CE,则可判断OC∥AD,根据平行线的性质得∠1=∠3,由于∠2=∠3,所以∠1=∠2.
解答 证明:连结OC,如图, ∵直线CE与⊙O相切于点C,
∵直线CE与⊙O相切于点C,
∴OC⊥CE,
∵AD⊥CE,
∴OC∥AD,
∴∠1=∠3,
∵OA=OC,
∴∠2=∠3,
∴∠1=∠2,
∴AC平分∠DAB.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
12.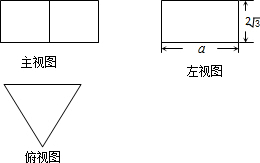 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
 一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )
一个正三棱柱的三视图如图所示,若这个正三棱柱的侧面积为8$\sqrt{3}$,则a的值为( )| A. | $\frac{2}{3}$$\sqrt{3}$ | B. | 2+$\frac{\sqrt{3}}{3}$ | C. | $\frac{3}{2}$ | D. | 2 |
4.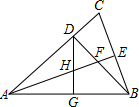 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
 如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )
如图,△ABC中,AB=AC,∠BAC=45°,BD⊥AC,垂足为D点,AE平分∠BAC,交BD于F,交BC于E,点G为AB的中点,连接DG,交AE于点H,下列结论错误的是( )| A. | AH=2DF | B. | AF=2HE | C. | AF=2CE | D. | DH=DF |
1.计算(-x3)2的结果是( )
| A. | -x5 | B. | x5 | C. | -x6 | D. | x6 |
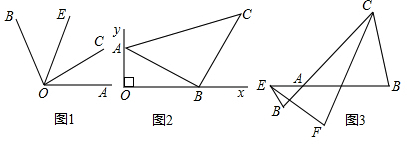
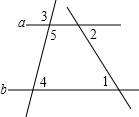 已知,如图所示,∠3=110°,∠4=70°,∠1=46°,求∠2的度数.
已知,如图所示,∠3=110°,∠4=70°,∠1=46°,求∠2的度数. 如图,线段AB=12cm,C是AB的中点.D是AC的中点,求DB.
如图,线段AB=12cm,C是AB的中点.D是AC的中点,求DB.