题目内容
12. 如图,直线AB∥CD,直线l分别交AB、CD于点E、F,EM平分∠BEF,∠EFD=50°,∠MEN=90°,求∠NEF的度数.
如图,直线AB∥CD,直线l分别交AB、CD于点E、F,EM平分∠BEF,∠EFD=50°,∠MEN=90°,求∠NEF的度数.
分析 先利用平行线的性质得到∠BEF=180°-∠EFD=130°,再利用角平分线定义得到∠MEF=$\frac{1}{2}$∠BEF=65°,然后根据互余计算∠NEF的度数.
解答 解:∵AB∥CD,
∴∠BEF+∠EFD=180°,
∴∠BEF=180°-50°=130°,
∵EM平分∠BEF,
∴∠MEF=$\frac{1}{2}$∠BEF=65°,
∵∠MEN=90°,
∴∠NEF=90°-65°=25°.
点评 本题考查了平行线性质:两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了角平分线定义.

练习册系列答案
相关题目
2.不等式组$\left\{\begin{array}{l}{3x-1≥5}\\{2x+4<x+7}\end{array}\right.$的解集为( )
| A. | x≥2 | B. | x<3 | C. | 2≤x<3 | D. | x>3 |
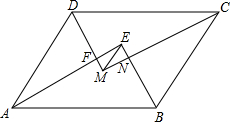 如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.
如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm. 如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=125°,求∠DFB和∠DGB的度数.
如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=125°,求∠DFB和∠DGB的度数. 如图,在矩形ABCD中,BE⊥AC于点E,DF⊥AC于点F,如果AE=1,EF=2,那么FC的长度是1,AB的长度是2.
如图,在矩形ABCD中,BE⊥AC于点E,DF⊥AC于点F,如果AE=1,EF=2,那么FC的长度是1,AB的长度是2.