题目内容
3.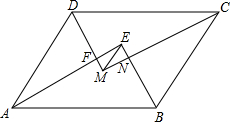 如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.
如图,?ABCD中,AB>AD,AE,BE,CM,DM分别为∠DAB,∠ABC,∠BCD,∠CDA的平分线,AE与DM相交于点F,BE与CM相交于点N,连接EM.若?ABCD的周长为42cm,FM=6cm,EF=8cm,则EM=10cm,AB=15.5cm.
分析 由条件易证∠AEB=∠AFD=∠DMC=90°.进而可证到四边形EFMN是矩形及∠EFM=90°,由FM=6cm,EF=8cm可求出EM.易证△ADF≌△CBN,从而得到DF=BN;易证△AFD∽△AEB,从而得到8DF=6AF.设DF=6k,则AF=8k.AE=8(k+1),BE=6(k+1),从而有AD=10k,AB=10(k+1).由?ABCD的周长为42cm可求出k,从而求出AB长.
解答 解:∵AE为∠DAB的平分线,
∴∠DAE=∠EAB=$\frac{1}{2}$∠DAB,
同理:∠ABE=∠CBE=$\frac{1}{2}$∠ABC,
∠BCM=∠DCM=$\frac{1}{2}$∠BCD,
∠CDM=∠ADM=$\frac{1}{2}$∠ADC.
∵四边形ABCD是平行四边形,
∴∠DAB=∠BCD,∠ABC=∠ADC,AD=BC.
∴∠DAF=∠BCN,∠ADF=∠CBN.
在△ADF和△CBN中,
$\left\{\begin{array}{l}{∠DAF=∠BCN}\\{AD=BC}\\{∠ADF=∠CBN}\end{array}\right.$
∴△ADF≌△CBN(ASA).
∴DF=BN.
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB+∠ABC=180°.
∴∠EAB+∠EBA=90°.
∴∠AEB=90°.
同理可得:∠AFD=∠DMC=90°.
∴∠EFM=90°.
∵FM=6,EF=8,
∴ME=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm).
∵∠EFM=∠FMN=∠FEN=90°.
∴四边形EFMN是矩形.
∴EN=FM=6.
∵∠DAF=∠EAB,∠AFD=∠AEB,
∴△AFD∽△AEB.
∴$\frac{DF}{BE}$=$\frac{AF}{AE}$.
∴$\frac{DF}{6+DF}$=$\frac{AF}{8+AF}$.
∴8DF=6AF.
设DF=6k,则AF=8k.
∵∠AFD=90°,
∴AD=10k.
∵∠AEB=90°,AE=8(k+1),BE=6(k+1),
∴AB=10(k+1).
∵2(AB+AD)=42,
∴AB+AD=21.
∴10(k+1)+10k=21.
∴k=0.55.
∴AB=15.5(cm).
故答案为:10;15.5.
点评 本题考查了平行四边形的性质、平行线的性质、矩形的判定与性质、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等知识,综合性较强.

 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案| A. | 3ac | B. | -3ac | C. | $\frac{1}{3}$ac | D. | -$\frac{1}{3}$ac |

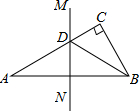 如图,在△ABC中,∠C=90°,AC=18cm,AB的垂直平分线MN交AC于D,连结BD,若$\frac{CB}{DB}=\frac{3}{5}$,则BC的长是( )
如图,在△ABC中,∠C=90°,AC=18cm,AB的垂直平分线MN交AC于D,连结BD,若$\frac{CB}{DB}=\frac{3}{5}$,则BC的长是( ) 已知:在直角坐标系中,直线y=x+1与x轴交于点A,与y轴交于点B,抛物线y=$\frac{1}{2}$(x-m)2+n的顶点D在直线AB上,与y轴的交点为C
已知:在直角坐标系中,直线y=x+1与x轴交于点A,与y轴交于点B,抛物线y=$\frac{1}{2}$(x-m)2+n的顶点D在直线AB上,与y轴的交点为C 如图,在正方形ABCD中,AB=a,M为AB的中点,ED=3AE.
如图,在正方形ABCD中,AB=a,M为AB的中点,ED=3AE. 如图,直线AB∥CD,直线l分别交AB、CD于点E、F,EM平分∠BEF,∠EFD=50°,∠MEN=90°,求∠NEF的度数.
如图,直线AB∥CD,直线l分别交AB、CD于点E、F,EM平分∠BEF,∠EFD=50°,∠MEN=90°,求∠NEF的度数. 如图所示,直线AF分别截BD、CE于G、H,点B在AC上,若∠1=∠2,∠C=∠D,则DF与AC平行吗?为什么?
如图所示,直线AF分别截BD、CE于G、H,点B在AC上,若∠1=∠2,∠C=∠D,则DF与AC平行吗?为什么?