题目内容
6. 如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.
如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.
分析 方案一:已知等边及垂直,在直角三角形中,可考虑ASA证明三角形全等,从而推出线段相等.
方案二:首先确定两点,使它们所在直线几乎垂直河岸;用标杆大致摆出AC的位置,交河岸于C点,再作AC的平行线BD(射线)在BD上取一点D,连接CD,使AB∥CD,再测量CD的长就可以了.
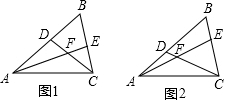
解答  解:方案一:如图1,在B点同侧取一点D,过点D作BD的垂线垂足为点D,
解:方案一:如图1,在B点同侧取一点D,过点D作BD的垂线垂足为点D,
取线段BD的中点O,延长AO交过点D的垂线于点C,
在△ABO和△CDO中
∵$\left\{\begin{array}{l}{∠ABO=∠CDO}\\{BO=DO}\\{∠BOA=∠DOC}\end{array}\right.$,
∴△ABO≌△CDO(ASA),
∴DC=AB,
量出DC的长,即可得出AB之间的距离;
方案二:如图2,首先确定两点,使它们所在直线几乎垂直河岸;用标杆大致摆出AC的位置,交河岸于C点,再作AC的平行线BD(射线)在BD上取一点D,连接CD,使AB∥CD,再测量CD的长就可以了.
点评 此题主要考查了应用设计与作图以及全等三角形的应用.在实际生活中,对于难以实地测量的线段,常常通过两个全等三角形,转化需要测量的线段到易测量的边上或者已知边上来,从而求解.

练习册系列答案
相关题目
14.$\sqrt{2a}$•$\sqrt{6ab}$等于( )
| A. | a $\sqrt{12ab}$ | B. | 12a2b | C. | a2$\sqrt{12b}$ | D. | 2a $\sqrt{3b}$ |
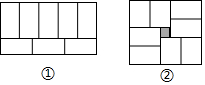 小亮用8个同样大小的长方形,拼成了一个大的长方形(图①).小莹用这8个长方形拼成了正方形(图②),但是中间空出了一个边长为2的小正方形,你能根据图①和图②求出小长方形的长和宽吗?
小亮用8个同样大小的长方形,拼成了一个大的长方形(图①).小莹用这8个长方形拼成了正方形(图②),但是中间空出了一个边长为2的小正方形,你能根据图①和图②求出小长方形的长和宽吗? 如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米.
如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小刚的身高为1.6米,那么路灯甲的高为8米. 有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.
有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程. 如图,AB∥CD,AD=BC,猜想∠BCD与∠ADC有什么关系?请说明理由.
如图,AB∥CD,AD=BC,猜想∠BCD与∠ADC有什么关系?请说明理由.