题目内容
16. 如图,AB∥CD,AD=BC,猜想∠BCD与∠ADC有什么关系?请说明理由.
如图,AB∥CD,AD=BC,猜想∠BCD与∠ADC有什么关系?请说明理由.
分析 结论:∠BCD=∠ADC.作BE∥AD交CD的延长线于E.首先证明四边形ABED是平行四边形,推出AD=BE=BC,推出∠BCD=∠E=∠ADC.
解答 解:结论:∠BCD=∠ADC.
理由:作BE∥AD交CD的延长线于E.
∵AB∥DE,AD∥BE,
∴四边形ABED是平行四边形,
∴AD=BE,∵AD=BC,
∴BC=BE,
∴∠BCE=∠E,
∵∠ADC=∠E,
∴∠BCD=∠ADC.
点评 本题考查平行四边形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造特殊四边形解决问题,属于中考常考题型.

练习册系列答案
相关题目
1.下面说法中,不正确的是( )
| A. | 绝对值最小的实数是0 | B. | 立方根最小的实数是0 | ||
| C. | 平方最小的实数是0 | D. | 算术平方根最小的实数是0 |
5.在Rt△ABC中,∠C=90°,AC=3,BC=4,那么sinB的值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
 如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.
如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.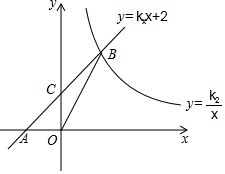 如图,在平面直角坐标系中,一次函数y=k1x+2的图象与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B,连结BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.
如图,在平面直角坐标系中,一次函数y=k1x+2的图象与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B,连结BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.