题目内容
15.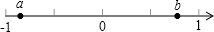 有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.
有两个十分喜欢探究的同学小明和小芳,他们善于将所做的题目进行归类,下面是他们的探究过程.(1)解题与归纳
①小明摘选了以下各题,请你帮他完成填空.$\sqrt{2^2}$=2; $\sqrt{5^2}$=5; $\sqrt{6^2}$=6;$\sqrt{0^2}$=0; $\sqrt{{{({-3})}^2}}$=3; $\sqrt{{{({-6})}^2}}$=6;
②归纳:对于任意数a,有$\sqrt{a^2}$=|a|=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$
③小芳摘选了以下各题,请你帮她完成填空.$(\sqrt{4}{)^2}$=4; $(\sqrt{9}{)^2}$=9; $(\sqrt{25}{)^2}$=25;$(\sqrt{36}{)^2}$=36;$(\sqrt{49}{)^2}$=49; $(\sqrt{0}{)^2}$=0;
④归纳:对于任意非负数a,有$(\sqrt{a}{)^2}$=a
(2)应用
根据他们归纳得出的结论,解答问题.
数a,b在数轴上的位置如图所示,化简:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$-$(\sqrt{b-a}{)^2}$.
分析 (1)根据要求填空即可;
(2)先根据数轴上点的位置确定:a<0,b>0,b>a,再根据(1)中的公式代入计算即可.
解答 解:(1)$\sqrt{2^2}$=2; $\sqrt{5^2}$=5; $\sqrt{6^2}$=6;$\sqrt{0^2}$=0; $\sqrt{{{({-3})}^2}}$=|-3|=3; $\sqrt{{{({-6})}^2}}$=|-6|=6;
故答案为:2,5,6,0,3,6;
②对于任意数a,有$\sqrt{a^2}$=|a|=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$,
故答案为:|a|=$\left\{\begin{array}{l}{a(a>0)}\\{0(a=0)}\\{-a(a<0)}\end{array}\right.$;
③$(\sqrt{4}{)^2}$=4; $(\sqrt{9}{)^2}$=9; $(\sqrt{25}{)^2}$=25;$(\sqrt{36}{)^2}$=36;$(\sqrt{49}{)^2}$=49; $(\sqrt{0}{)^2}$=0;
故答案为:4,9,25,36,49,0
④对于任意非负数a,有$(\sqrt{a}{)^2}$=a,
故答案为:a;
(2)由数轴得:a<0,b>0,b>a,
∴b-a>0
化简:$\sqrt{{a}^{2}}$-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$-$(\sqrt{b-a}{)^2}$.
=|a|-|b|+|a-b|-(b-a)
=-a-b+b-a-b+a
=-a-b.
点评 本题属于阅读理解问题,主要考查了算术平方根和平方的定义、数轴的知识,正确把握算术平方根定义是解题关键.

| A. | 最小的有理数是0 | |
| B. | 射线OM的长度是5cm | |
| C. | 两数相加,和一定大于任何一个加数 | |
| D. | 两点确定一条直线 |
| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
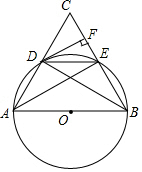 如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且$\widehat{AD}$=$\widehat{DE}$,过点D作DF⊥BC于点F,连接BD、DE、AE.
如图,AB为⊙O的直径,点C为圆外一点,连接AC、BC,分别与⊙O相交于点D、点E,且$\widehat{AD}$=$\widehat{DE}$,过点D作DF⊥BC于点F,连接BD、DE、AE. 如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.
如图是一条河,A、B是对岸两点(AB垂直河岸),某同学站在B点,在不能到达对岸的情况下,请你帮他设计至少两种方案求出A、B之间的距离,并请说明理由.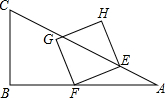 如图,在△ABC中,∠B=90°,AB=4,BC=2,点E从点A出发,以每秒$\sqrt{5}$个单位长度的速度沿边AC向终点C运动,E点出发的同时,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F逆时针旋转90°得到线段FG,以EF、FG为边作正方形EFGH,设点F运动的时间为t秒(t>0)
如图,在△ABC中,∠B=90°,AB=4,BC=2,点E从点A出发,以每秒$\sqrt{5}$个单位长度的速度沿边AC向终点C运动,E点出发的同时,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F逆时针旋转90°得到线段FG,以EF、FG为边作正方形EFGH,设点F运动的时间为t秒(t>0)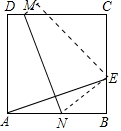 如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.
如图,在正方形ABCD中,E是BC的中点,折叠正方形使点A与E重合,折痕为MN,若梯形ADMN的面积是$\frac{3}{2}$,则正方形的边长是2;梯形ADMN与梯形BCMN的面积之比是$\frac{3}{5}$.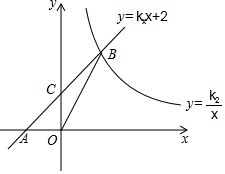 如图,在平面直角坐标系中,一次函数y=k1x+2的图象与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B,连结BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.
如图,在平面直角坐标系中,一次函数y=k1x+2的图象与x轴交于点A,与y轴交于点C,与反比例函数y=$\frac{{k}_{2}}{x}$的图象在第一象限内交于点B,连结BO.若S△OBC=1,tan∠BOC=$\frac{1}{3}$.