题目内容
 如图,在△ABC中,∠ACB=90°,AC=2,BC=2
如图,在△ABC中,∠ACB=90°,AC=2,BC=2| 3 |
考点:轴对称-最短路线问题
专题:
分析:先求得F和C关于AE对称,进而证得P和E重合时,PB+PF=BC最小,因为BF是定值,此时△BFP周长的最小,然后根据周长公式即可求得.
解答:解:∵在△ABC中,∠ACB=90°,AC=2,∠B=30°,
∴AB=4,
∵F为AB的中点,
∴AF=BF=AC=2,
∵AE平分∠BAC,
∴C、F关于AE对称,
∴当P和E重合时,PB+PF=BC最小,因为BF是定值,此时△BFP周长的最小,
∴△BFP周长的最小值=PB+PE+BF=BC+BF=2+2
.
故答案为2+2
.
∴AB=4,
∵F为AB的中点,
∴AF=BF=AC=2,
∵AE平分∠BAC,
∴C、F关于AE对称,
∴当P和E重合时,PB+PF=BC最小,因为BF是定值,此时△BFP周长的最小,
∴△BFP周长的最小值=PB+PE+BF=BC+BF=2+2
| 3 |
故答案为2+2
| 3 |
点评:本题考查了30°角的直角三角形的性质,轴对称的性质,根据两点之间线段最短求得PB+PF的最小值是本题的关键.

练习册系列答案
相关题目
一个两位数,个位上的数字比十位上的数字小4,且个位数字与十位数字的平方和比这个两位数大4.设个位数字为x,则方程为( )
| A、x2+(x-4)2=10(x-4)+x-4 |
| B、x2+(x-4)2=10(x-4)+x+4 |
| C、x2+(x-4)2=10x+x-4-4 |
| D、x2+(x+4)2=10(x+4)+x+4 |
 如图,⊙O是△ABC的外接圆,AB为直径,
如图,⊙O是△ABC的外接圆,AB为直径,
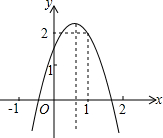 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①abc<0;②-a<b<-2a;③b2+8a>4ac;④a<-1.其中正确的结论有
如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1,x2,其中-1<x1<0,1<x2<2.下列结论:①abc<0;②-a<b<-2a;③b2+8a>4ac;④a<-1.其中正确的结论有 如图,点M,N是第一象限内的两点,坐标分别为M(2,3),N(4,0)
如图,点M,N是第一象限内的两点,坐标分别为M(2,3),N(4,0) 如图,已知抛物线y=-x2+4x+m与x轴交于A,B两点,AB=2,与y轴交于C.
如图,已知抛物线y=-x2+4x+m与x轴交于A,B两点,AB=2,与y轴交于C.