题目内容
 如图,点M,N是第一象限内的两点,坐标分别为M(2,3),N(4,0)
如图,点M,N是第一象限内的两点,坐标分别为M(2,3),N(4,0)(1)若点P是y轴上的一个动点,当△PMN周长最小时,求点P的坐标.
(2)若P,Q是y轴上的两点(点P在Q的下方),且PQ=1,当四边形PQMN周长最小时,点P的坐标.
考点:轴对称-最短路线问题,坐标与图形性质
专题:
分析:(1)根据轴对称,作出点M关于y轴的对称点M′,连接M′N交y轴于点P,此时△PMN周长最小,求得M′的坐标,然后利用待定系数法求得直线M′N的解析式,即可求得P的坐标;
(2)根据轴对称,作出点M关于y轴的对称点A,作AB∥y轴且AB=1,连接BN交y轴于点P,过A作AQ∥BP交y轴于Q,此时四边形PQMN周长最小,求得B点的坐标,然后利用待定系数法求得直线BN的解析式,即可求得P的坐标;
(2)根据轴对称,作出点M关于y轴的对称点A,作AB∥y轴且AB=1,连接BN交y轴于点P,过A作AQ∥BP交y轴于Q,此时四边形PQMN周长最小,求得B点的坐标,然后利用待定系数法求得直线BN的解析式,即可求得P的坐标;
解答: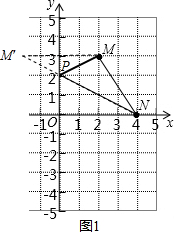 解:(1)如图1所示:作出点M关于y轴的对称点M′,连接M′N交y轴于点P,此时M′N就是PM+PN的最小值,由于MN是定值,所以此时△PMN周长最小,
解:(1)如图1所示:作出点M关于y轴的对称点M′,连接M′N交y轴于点P,此时M′N就是PM+PN的最小值,由于MN是定值,所以此时△PMN周长最小,
由题意可得出:M′(-2,3),
∵N(4,0),
设直线M′N的解析式为y=kx+b,
∴
,解得
,
∴直线M′N的解析式为y=-
x+2,
令x=0,则y=2,
∴P的坐标为(0,2);
(2)如图2所示:作出点M关于y轴的对称点A,作AB∥y轴且AB=1,连接BN交y轴于点P,过A作AQ∥BP交y轴于Q,此时BN就是QM+PN的最小值,由于MN、PQ是定值,所以此时四边形PQMN周长最小,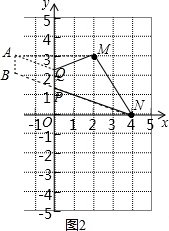
由题意可得出:A(-2,3),
∵AB=PQ=1,
∴B(-2,2)
∵N(4,0),
设直线BN的解析式为y=mx+n,
∴
,解得
,
∴直线BN的解析式为y=-
x+
,
令x=0,则y=
,
∴P的坐标为(0,
).
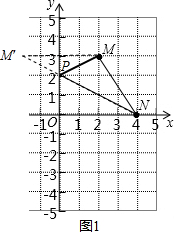 解:(1)如图1所示:作出点M关于y轴的对称点M′,连接M′N交y轴于点P,此时M′N就是PM+PN的最小值,由于MN是定值,所以此时△PMN周长最小,
解:(1)如图1所示:作出点M关于y轴的对称点M′,连接M′N交y轴于点P,此时M′N就是PM+PN的最小值,由于MN是定值,所以此时△PMN周长最小,由题意可得出:M′(-2,3),
∵N(4,0),
设直线M′N的解析式为y=kx+b,
∴
|
|
∴直线M′N的解析式为y=-
| 1 |
| 2 |
令x=0,则y=2,
∴P的坐标为(0,2);
(2)如图2所示:作出点M关于y轴的对称点A,作AB∥y轴且AB=1,连接BN交y轴于点P,过A作AQ∥BP交y轴于Q,此时BN就是QM+PN的最小值,由于MN、PQ是定值,所以此时四边形PQMN周长最小,

由题意可得出:A(-2,3),
∵AB=PQ=1,
∴B(-2,2)
∵N(4,0),
设直线BN的解析式为y=mx+n,
∴
|
|
∴直线BN的解析式为y=-
| 1 |
| 3 |
| 4 |
| 3 |
令x=0,则y=
| 4 |
| 3 |
∴P的坐标为(0,
| 4 |
| 3 |
点评:此题主要考查了利用轴对称求最短路线,待定系数法求解析式以及一次函数图象上点的特征等知识,得出P点位置是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
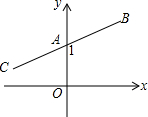 如图,点A,点B的坐标分别是(0,1),(a,b),将线段AB绕A旋转180°后得到线段AC,则点C的坐标为( )
如图,点A,点B的坐标分别是(0,1),(a,b),将线段AB绕A旋转180°后得到线段AC,则点C的坐标为( )| A、(-a,-b+1) |
| B、(-a,-b-1) |
| C、(-a,-b+2) |
| D、(-a,-b-2) |
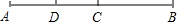 如图,C,D是线段AB上两点,若CB=5cm,DB=9cm,且D是AC的中点,则AC=
如图,C,D是线段AB上两点,若CB=5cm,DB=9cm,且D是AC的中点,则AC= 如图,在△ABC中,∠ACB=90°,AC=2,BC=
如图,在△ABC中,∠ACB=90°,AC=2,BC=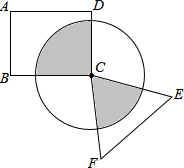 如图,四边形ABCD是矩形,△CEF是正三角形,⊙C的半径为2,求阴影部分的面积.
如图,四边形ABCD是矩形,△CEF是正三角形,⊙C的半径为2,求阴影部分的面积.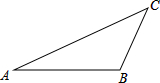 (1)已知:如图,△ABC,求作:点P,使得PC∥AB,且△ABP是以AB为底的等腰三角形(要求:尺规左图,保留作图痕迹)
(1)已知:如图,△ABC,求作:点P,使得PC∥AB,且△ABP是以AB为底的等腰三角形(要求:尺规左图,保留作图痕迹)