题目内容
 如图,已知抛物线y=-x2+4x+m与x轴交于A,B两点,AB=2,与y轴交于C.
如图,已知抛物线y=-x2+4x+m与x轴交于A,B两点,AB=2,与y轴交于C.(1)求抛物线解析式;
(2)求P为对称轴上一点,要使PA+PC最小,求点P的坐标.
考点:待定系数法求二次函数解析式,轴对称-最短路线问题
专题:计算题
分析:(1)先根据二次函数的性质求出抛物线的对称轴为直线x=2,则可利用抛物线的对称性确定A点坐标为(1,0),B点坐标为(3,0),于是可利用交点式写出抛物线解析式;
(2)连结BC,交直线x=2于点P,则PA=PB,PA+PC=PB+PC=BC,利用两点之间线段最短确定此时PA+PC最小,再利用待定系数法求出直线BC的解析式,然后求出自变量为2时的函数值即可得到点P的坐标.
(2)连结BC,交直线x=2于点P,则PA=PB,PA+PC=PB+PC=BC,利用两点之间线段最短确定此时PA+PC最小,再利用待定系数法求出直线BC的解析式,然后求出自变量为2时的函数值即可得到点P的坐标.
解答: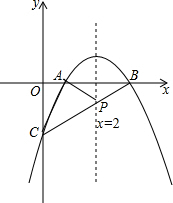 解:(1)抛物线的对称轴为直线x=-
解:(1)抛物线的对称轴为直线x=-
=2,
∵点A与点B是抛物线的对称点,
而AB=2,
∴A点坐标为(1,0),B点坐标为(3,0),
∴抛物线解析式为y=-(x-1)(x-3)=-x2+4x-3;
(2)连结BC,交直线x=2于点P,则PA=PB,
∴PA+PC=PB+PC=BC,
∴此时PA+PC最小,
设直线BC的解析式为y=kx+b,
把C(0,-3),B(3,0)代入得
,解得
,
∴直线BC的解析式为y=x-3,
当x=2时,y=x-3=2-3=-1,
∴P点坐标为(2,-1).
 解:(1)抛物线的对称轴为直线x=-
解:(1)抛物线的对称轴为直线x=-| 4 |
| 2×(-1) |
∵点A与点B是抛物线的对称点,
而AB=2,
∴A点坐标为(1,0),B点坐标为(3,0),
∴抛物线解析式为y=-(x-1)(x-3)=-x2+4x-3;
(2)连结BC,交直线x=2于点P,则PA=PB,
∴PA+PC=PB+PC=BC,
∴此时PA+PC最小,
设直线BC的解析式为y=kx+b,
把C(0,-3),B(3,0)代入得
|
|
∴直线BC的解析式为y=x-3,
当x=2时,y=x-3=2-3=-1,
∴P点坐标为(2,-1).
点评:本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
 如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )
如图是由几个相同的正方体搭成的一个几何体,从正面看到的平面图形是( )A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,∠ACB=90°,AC=2,BC=
如图,在△ABC中,∠ACB=90°,AC=2,BC=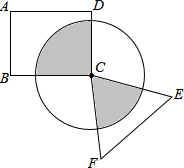 如图,四边形ABCD是矩形,△CEF是正三角形,⊙C的半径为2,求阴影部分的面积.
如图,四边形ABCD是矩形,△CEF是正三角形,⊙C的半径为2,求阴影部分的面积.
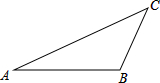 (1)已知:如图,△ABC,求作:点P,使得PC∥AB,且△ABP是以AB为底的等腰三角形(要求:尺规左图,保留作图痕迹)
(1)已知:如图,△ABC,求作:点P,使得PC∥AB,且△ABP是以AB为底的等腰三角形(要求:尺规左图,保留作图痕迹)