题目内容
如图，⊙O是△ABC的外接圆，AB为直径， |
| AC |
|
| CF |
（1）求证：AE=CE；
（2）若AD=2，BD=8，求AF的长．
考点：圆周角定理,勾股定理,垂径定理
专题：
分析：（1）如图，作辅助线；证明
=
，借助
=
，得到
=
，即可解决问题．
（2）如图，作辅助线；根据勾股定理求出CD；进而求出AE；证明△ADE∽△AFB，列出比例式即可解决问题．
|
| AC |
|
| AG |
|
| AC |
|
| CF |
|
| AG |
|
| CF |
（2）如图，作辅助线；根据勾股定理求出CD；进而求出AE；证明△ADE∽△AFB，列出比例式即可解决问题．
解答：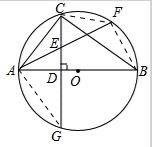
（1）证明：连接AG，CF．
∵AB为直径，且AB⊥CG，
∴
=
，
又∵
=
，
∴
=
，
∴∠ACG=∠CAF，
∴AE=CE．
（2）连接BF；
∵AB为直径，
∴∠ACB=90°，∠AFB=90°；而CD⊥AB，
∴CD2=AD•BD=16，
∴CD=4；设AE=CE=λ，
∴DE=4-λ，由勾股定理得：
λ2=22+（4-λ）2，
解得：λ=2.5，即AE=2.5．
∵∠FAB=∠EAD，∠EDA=∠BFA，
∴△ADE∽△AFB，
∴AE：AB=AD：AF，而AB=10，AD=2，AE=2.5，
∴AF=8．
（1）证明：连接AG，CF．∵AB为直径，且AB⊥CG，
∴
|
| AC |
|
| AG |
又∵
|
| AC |
|
| CF |
∴
|
| AG |
|
| CF |
∴∠ACG=∠CAF，
∴AE=CE．
（2）连接BF；
∵AB为直径，
∴∠ACB=90°，∠AFB=90°；而CD⊥AB，
∴CD2=AD•BD=16，
∴CD=4；设AE=CE=λ，
∴DE=4-λ，由勾股定理得：
λ2=22+（4-λ）2，
解得：λ=2.5，即AE=2.5．
∵∠FAB=∠EAD，∠EDA=∠BFA，
∴△ADE∽△AFB，
∴AE：AB=AD：AF，而AB=10，AD=2，AE=2.5，
∴AF=8．
点评：本题主要考查了垂径定理，圆周角定理．根据圆周角得出相关的角相等是本题的解题关键．
练习册系列答案
阅读快车系列答案
相关题目
一件商品按成本价提高40%后标价，再打8折（标价的80%）销售，售价为130元，设这件商品的成本价为x元，根据题意，下面所列方程正确的是（ ）
| A、40%×80%x=130 |
| B、40%x=130×80% |
| C、130×80%×40%=x |
| D、（1+40%）x×80%=130 |
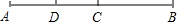如图，C，D是线段AB上两点，若CB=5cm，DB=9cm，且D是AC的中点，则AC=
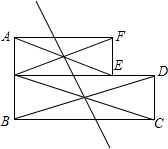如图是由两个矩形组成的组合图形，能否在图形中找到一点P，沿过点P的某一条直线折叠该图形，能将该图形分成面积相等的两部分？若能，请你在图中做出点P，并说明点P的位置；若不能，请说明理由．
如图，在△ABC中，∠ACB=90°，AC=2，BC=