题目内容
20.已知样本为101,98,102,100,99,则样本方差为( )| A. | 2 | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
分析 先求出这组数据的平均数,再利用方差公式S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2]计算即可.
解答 解:平均数$\overline{x}$=$\frac{1}{5}$(101+98+102+100+99)=100,
方差S2=$\frac{1}{5}$[(101-100)2+(98-100)2+(102-100)2+(100-100)2+(99-100)2]=2.
故选A.
点评 本题主要考查方差的定义.一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.下列由左到右的变形,属于因式分解的是( )
| A. | (x+3y)(x-3y)=x2-9y | B. | x2-3x+2=(x-1)(x-2) | ||
| C. | 3x2+6x-1=3x(x+2)-1 | D. | (x-2y)2=x2-4xy+4y2 |
5.已知xm=a,xn=b,那么xm+2n的值等于( )
| A. | a+2b | B. | a+b2 | C. | ab2 | D. | amb2n |
12.如果a>b,则下列不等式一定成立的是( )
| A. | 1-a>1-b | B. | -a>-b | C. | ac>bc | D. | a-2>b-2 |
9. 如图,将三角板的直角顶点放在直尺的一边上,若∠2=25°,则∠1的度数为( )
如图,将三角板的直角顶点放在直尺的一边上,若∠2=25°,则∠1的度数为( )
 如图,将三角板的直角顶点放在直尺的一边上,若∠2=25°,则∠1的度数为( )
如图,将三角板的直角顶点放在直尺的一边上,若∠2=25°,则∠1的度数为( )| A. | 75° | B. | 65° | C. | 55° | D. | 45° |
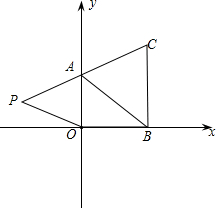 如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0和(c-4)2≤0;
如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0和(c-4)2≤0;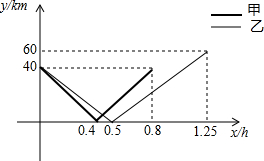 甲乙两车分别从A,B两地出发相向而行,途中经过一加油站C,若乙车先出发,甲乙两车车距加油站C的距离y(单位:cm)与甲车出发时间x(单位:h)的函数关系如图所示:
甲乙两车分别从A,B两地出发相向而行,途中经过一加油站C,若乙车先出发,甲乙两车车距加油站C的距离y(单位:cm)与甲车出发时间x(单位:h)的函数关系如图所示: