题目内容
10.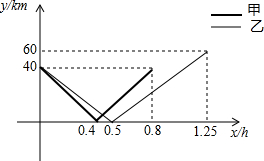 甲乙两车分别从A,B两地出发相向而行,途中经过一加油站C,若乙车先出发,甲乙两车车距加油站C的距离y(单位:cm)与甲车出发时间x(单位:h)的函数关系如图所示:
甲乙两车分别从A,B两地出发相向而行,途中经过一加油站C,若乙车先出发,甲乙两车车距加油站C的距离y(单位:cm)与甲车出发时间x(单位:h)的函数关系如图所示:(1)求两车的速度,及A,B两地之间的距离;
(2)求甲车距加油站C的距离y(单位:cm)与甲车出发时间x(单位:cm)之间的函数解析式;
(3)求乙车出发多长时间后两车相遇.
分析 (1)根据图象得出速度等于路程除以时间,同时也得出A,B两地之间的距离即可;
(2)根据待定系数法得出函数解析式即可;
(3)根据甲、乙的速度和AB的距离计算即可.
解答 解:(1)甲车的速度为:40÷0.4=100千米/小时;
乙车的速度为:40÷0.5=80千米/小时;
A,B两地之间的距离为:40+60=100千米;
(2)甲车距加油站C的距离y(单位:cm)与甲车出发时间x(单位:cm)之间的函数解析式为:$\left\{\begin{array}{l}{y=-100x+40(0≤x≤0.4)}\\{y=100x-40(0.4<x≤0.8)}\end{array}\right.$,
(3)100÷(100+80)=$\frac{5}{9}$,乙车出发$\frac{5}{9}$h后两车相遇.
点评 此题考查一次函数的应用,关键是根据一次函数的解析式进行计算.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
20.已知样本为101,98,102,100,99,则样本方差为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
1.下列说法不正确的是( )
| A. | 平行四边形的对角互补,邻角相等 | |
| B. | 平行四边形的对角线互相平分 | |
| C. | 有两组对边分别平行的四边形是平行四边形 | |
| D. | 平行四边形的对边平行且相等 |

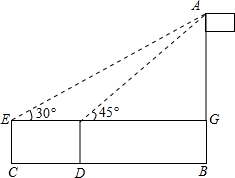 如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)
如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)