题目内容
10.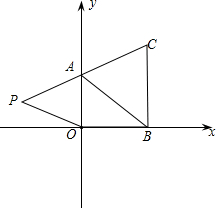 如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0和(c-4)2≤0;
如图,在下面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a、b、c满足关系式|a-2|+(b-3)2=0和(c-4)2≤0;(1)求a、b、c的值;
(2)如果在第二象限内有一点p(m,$\frac{1}{3}$),请用含m的式子表示四边形ABOP的面积;
(3)在(2)的条件下,是否存在点P,使得四边形ABOP的面积与△ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
分析 (1)根据非负数的性质,即可解答;
(2)四边形ABOP的面积=△APO的面积+△AOB的面积,即可解答;
(3)存在,根据面积相等求出m的值,即可解答.
解答 解:(1)由已知|a-2|+(b-3)2=0,(c-4)2≤0可得:
a-2=0,b-3=0,c-4=0,
解得:a=2,b=3,c=4;
(2)∵a=2,b=3,c=4,
∴A(0,2),B(3,0),C(3,4),
∴OA=2,OB=3,
∵S△ABO=$\frac{1}{2}$×2×3=3,
S△APO=$\frac{1}{2}$×2×(-m)=-m,
∴S四边形ABOP=S△ABO+S△APO=3+(-m)=3-m
(3)存在,
∵S△ABC=$\frac{1}{2}$×4×3=6,
若S四边形ABOP=S△ABC=3-m=6,则m=-3,
∴存在点P(-3,$\frac{1}{3}$)使S四边形ABOP=S△ABC.
点评 本题考查了坐标与图形性质,解决本题的关键是根据非负数的性质求出a,b,c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.小米同学乘坐一艘游船出海游玩,游船上的雷达扫描探测得到的结果如图所示,每相邻两个圆之间距离是1km(小圆半径是1km),若小艇C相对于游船的位置可表示为(0°,-1.5),请你描述图中另外两个小艇A、B的位置,正确的是( )
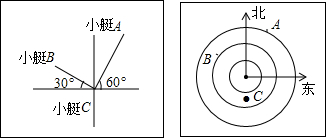

| A. | 小艇A(60°,3),小艇B(-30°,2) | B. | 小艇A(30°,4),小艇B(-60°,3) | ||
| C. | 小艇A(60°,3),小艇B(-30°,3) | D. | 小艇A(30°,3),小艇B(-60°,2) |
5.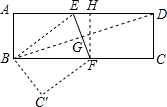 如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )
如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )
 如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )
如图,矩形ABCD的长AD=9cm,宽AB=3cm,将它折叠,使点D与点B重合,求折叠后DE的长和EF的长分别是( )| A. | 5cm,3cm | B. | 5cm,$\sqrt{10}$cm | C. | 6cm,$\sqrt{10}$cm | D. | 5cm,4cm |
19.2015年2月份,泗阳某周的日最高气温统计如下(单位:℃):2、4、5、3、4、6、7,则这七天中日最高气温的众数和中位数分别是( )
| A. | 4℃,4℃ | B. | 5℃,4℃ | C. | 4℃,3℃ | D. | 4℃,4.5℃ |
20.已知样本为101,98,102,100,99,则样本方差为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 0 | D. | 1 |
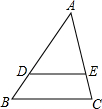 如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,△ABC的面积为
如图,△ABC中,点D、E分别在AB、AC边上,DE∥BC,若AD:AB=3:4,△ABC的面积为 如图所示,矩形纸片ABCD中,AB=5cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=10 cm.
如图所示,矩形纸片ABCD中,AB=5cm,点E在BC上,且AE=EC.若将纸片沿AE折叠,点B恰好与AC上的点B′重合,则AC=10 cm.