题目内容
 如图,AB是⊙O直径,∠AOC=130°,则∠D=
如图,AB是⊙O直径,∠AOC=130°,则∠D=考点:圆周角定理
专题:
分析:由AB是⊙O直径,∠AOC=130°,根据邻补角的定义,即可求得∠BOC的度数,然后根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠D的度数.
解答:解:∵AB是⊙O直径,∠AOC=130°,
∴∠BOC=180°-∠AOC=50°,
∴∠D=
∠BOC=25°.
故答案为:25.
∴∠BOC=180°-∠AOC=50°,
∴∠D=
| 1 |
| 2 |
故答案为:25.
点评:此题考查了圆周角定理.此题比较简单,解题的关键是掌握在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半定理的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某地区的消费品零售总额持续增长,10月份为1.2亿元,11月份达到2.8亿元,如果从9月份到11月份每月增长的百分率相同,则9月份的消费品零售总额为( )
A、2.8×(1-
| ||
B、2.8×(1-
| ||
C、2.8÷(1+
| ||
D、2.8÷(1+
|
直线l与直线y=-2x+3平行,并且与直线y=2x-3交于y轴的同一点,则直线l的解析式为( )
| A、y=-2x-3 |
| B、y=-2x+3 |
| C、y=2x-3 |
| D、y=2x+3 |
直线l外一点P与直线l上两点的连线段长分别为4cm,6cm,则点P到直线l的距离是( )
| A、不超过4cm | B、4cm |
| C、6cm | D、不少于6cm |
 如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).
如图,小明和小刚的家分别在A﹑B两地,ON是去往学校的马路,他们每次上学时都约在ON上一点C,这一点与他们家的距离分别相等.请用尺规作图的方法在图中作出点C(保留作图痕迹).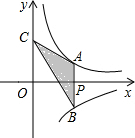 如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=
如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y= 如图,AB=AC,BD=CD,延长DB至M,使MB=
如图,AB=AC,BD=CD,延长DB至M,使MB=