题目内容
如图，AB∥CD，| AO |
| OD |
| 2 |
| 3 |
考点：相似三角形的判定与性质
专题：
分析：根据相似三角形周长的比等于相似比即可求得．
解答：解：∵AB∥CD
∴△AOB∽△DOC
∴OA：OD=OB：OC
∵
=
，
∴△AOB与△DOC的周长比是2：3，
故答案为2：3．
∴△AOB∽△DOC
∴OA：OD=OB：OC
∵
| AO |
| OD |
| 2 |
| 3 |
∴△AOB与△DOC的周长比是2：3，
故答案为2：3．
点评：本题考查相似三角形判定和性质，相似三角形周长的比等于相似比是本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
某地区的消费品零售总额持续增长，10月份为1.2亿元，11月份达到2.8亿元，如果从9月份到11月份每月增长的百分率相同，则9月份的消费品零售总额为（ ）
A、2.8×(1-
| ||
B、2.8×(1-
| ||
C、2.8÷(1+
| ||
D、2.8÷(1+
|
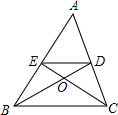△ABC中，中线BD与CE相交于O点，S△ADE=1，则S四边形BCDE=
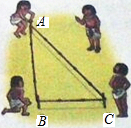相传，古埃及人用13个等距的结把一根绳子分成等长的12段．并把它摆成△ABC的形状，如图所示，工人们按这种造型在金字塔等建筑的拐角作出直角，试问这种“张绳法”能否得到一个直角三角形呢？请同学们动手试一试，并说明理由．
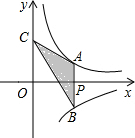如图，过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=