题目内容
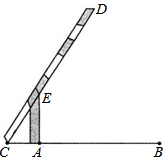 如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据:
如图,小明在研究性学习活动中,对自己家所在的小区进行调查后发现,小区汽车入口宽AB为3.2m,在入口的一侧安装了停止杆CD,其中AE为支架.当停止杆仰起并与地面成60°角时,停止杆的端点C恰好与地面接触.此时CA为0.7m.在此状态下,若一辆货车高3m,宽2.5m,入口两侧不能通车,那么这辆货车在不碰杆的情况下,能从入口内通过吗?请你通过估算说明.(参考数据:| 3 |
考点:二次根式的应用
专题:
分析:首先在AB之间找一点F,且BF=2.5,过点F作GF⊥AB交CD于点G,只要求得GF的数值,进一步与货车高相比较得出答案即可.
解答:解:如图,
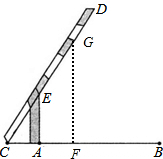
在AB之间找一点F,使BF=2.5m,过点F作GF⊥AB交CD于点G,
∵AB=3.2m,CA=0.7m,BF=2.5m,
∴CF=AB-BF+CA=1.4m,
∵∠ECA=60°,
∴tan60°=
,
∴GF=CAtan60°=1.4
≈2.38m,
∵2.38<3
∴这辆货车在不碰杆的情况下,不能从入口内通过.

在AB之间找一点F,使BF=2.5m,过点F作GF⊥AB交CD于点G,
∵AB=3.2m,CA=0.7m,BF=2.5m,
∴CF=AB-BF+CA=1.4m,
∵∠ECA=60°,
∴tan60°=
| GF |
| CA |
∴GF=CAtan60°=1.4
| 3 |
∵2.38<3
∴这辆货车在不碰杆的情况下,不能从入口内通过.
点评:此题考查二次根式的运用以及锐角三角函数的实际运用,理解题意,结合图形,选用适当的方法解决问题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
直线l与直线y=-2x+3平行,并且与直线y=2x-3交于y轴的同一点,则直线l的解析式为( )
| A、y=-2x-3 |
| B、y=-2x+3 |
| C、y=2x-3 |
| D、y=2x+3 |
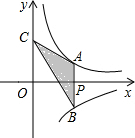 如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y=
如图,过x轴正半轴上的任意一点P作y轴的平行线交反比例函数y= 已知:如图,点A、B、D、E在同一直线上,AD=EB,AC=EF,AC∥EF.求证:BC=DF.
已知:如图,点A、B、D、E在同一直线上,AD=EB,AC=EF,AC∥EF.求证:BC=DF. 如图,AB=AC,BD=CD,延长DB至M,使MB=
如图,AB=AC,BD=CD,延长DB至M,使MB=