题目内容
12.(1)计算:(5$\sqrt{2}$-2$\sqrt{3}$)2-(3$\sqrt{2}$-$\sqrt{5}$)(3$\sqrt{2}$+$\sqrt{5}$).(2)解方程:x(x+4)=8x+12.
分析 (1)先根据乘法公式计算出乘法,然后合并同类二次根式;
(2)先把方程整理为一般式得x2-4x-12=0,再把方程左边分解得(x+2)(x-6)=0,原方程转化为x+2=0或x-6=0,然后解一次方程即可.
解答 解:(1)原式=50-20$\sqrt{6}$+12-(18-5)
=49-20$\sqrt{6}$;
(2)原方程变形为:x2-4x-12=0,
(x-6)(x+2)=0,
∴x-6=0,x+2=0,
∴x1=6,x2=-2.
点评 本题考查了二次根式的混合运算,熟练掌握运算顺序是关键;也考查了解一元二次方程-因式分解法:先把方程右边变形为0,再把方程左边分解为两个一次式的乘积,这样原方程转化为两个一元一次方程,然后解一次方程即可得到一元二次方程的解.

练习册系列答案
相关题目
20.如果每盒笔有18支,售价12元,用y(元)表示笔的售价,x表示笔的支数,那么y与x之间的关系式应该是( )
| A. | y=12x | B. | y=18x | C. | y=$\frac{2}{3}$x | D. | y=$\frac{3}{2}x$ |
17.已知单项式3am-1b2与-2ab1-m相加的结果还是单项式,则nm的值是( )
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
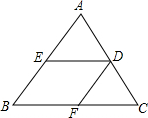 如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号)
如图,在△ABC中,DE∥BC,DF∥AB,那么下列比例式中正确的是①;(填序号) 如图,某小区有A、B、C、D四栋楼,现在要建造一个水塔P,请画出水塔P应建在何位置,才能使它到四栋楼的距离之和最小,说明画图的原理.
如图,某小区有A、B、C、D四栋楼,现在要建造一个水塔P,请画出水塔P应建在何位置,才能使它到四栋楼的距离之和最小,说明画图的原理. 如图,已知∠AOB,以O为圆心,以任意长为半径画弧,分别交OA、OB于D、E两点,再分别以D、E为圆心,大于$\frac{1}{2}$DE长为半径画弧,两条弧交于点C,作射线OC,则OC是∠AOB的角平分线吗?说明理由.
如图,已知∠AOB,以O为圆心,以任意长为半径画弧,分别交OA、OB于D、E两点,再分别以D、E为圆心,大于$\frac{1}{2}$DE长为半径画弧,两条弧交于点C,作射线OC,则OC是∠AOB的角平分线吗?说明理由. 如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.
如图,在每个小正方形的边长均为1的方格纸中有线段AB和CD,点A、B、C、D均在小正方形的顶点上.