Question

7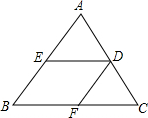．如图，在△ABC中，DE∥BC，DF∥AB，那么下列比例式中正确的是①；（填序号）
①$\frac{AE}{EB}$=$\frac{BF}{FC}$；②$\frac{AE}{EB}$=$\frac{CF}{FB}$；③$\frac{DE}{BC}$=$\frac{AD}{DC}$；④$\frac{DE}{BC}$=$\frac{DF}{AB}$．

Answer 1

分析 根据平行线分线段成比例定理，由DE∥BC得$\frac{AE}{EB}=\frac{AD}{CD}$，由DF∥AB得$\frac{AD}{CD}=\frac{BF}{FC}$，则$\frac{AE}{EB}=\frac{BF}{FC}$，于是可对A、B进行判断；再由DE∥BC得到$\frac{DE}{BC}=\frac{AD}{AC}$，则可对C进行判断；由DF∥AB得到$\frac{DF}{AB}=\frac{CD}{AC}$，所以$\frac{DE}{BC}=\frac{DF}{AB}$=1，于是可对D进行判断．

解答 解：∵DE∥BC，
∴$\frac{AE}{EB}=\frac{AD}{DC}$，
∵DF∥AB，
∴$\frac{AD}{CD}=\frac{BF}{FC}$，
∴$\frac{AE}{EB}=\frac{BF}{FC}$，所以①选项正确，②选项错误；
∵DE∥BC，
∴$\frac{DE}{BC}=\frac{AD}{AC}$，所以③选项错误；
∵DF∥AB，
∴$\frac{DF}{AB}=\frac{CD}{AC}$，
∴$\frac{DE}{BC}$+$\frac{DF}{AB}$=1，所以④选项错误．
故答案为：①．

点评 本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．