题目内容
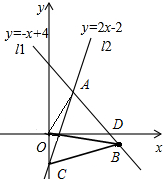
 直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x,
直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x,(1)求直线L1的解析式;
(2)若直线L2:y=2x-2与直线L1交与点A,与y轴交于点C,求由O,A,B,C四点组成的四边形构成的四边形的面积.
考点:两条直线相交或平行问题
专题:
分析:(1)根据两直线平行,可得k的值,再将(5,-1)代入解析式,确定b的值;
(2)先求出点C的坐标,再题意画出图形,根据图形求四边形的面积.
(2)先求出点C的坐标,再题意画出图形,根据图形求四边形的面积.
解答:解:(1)∵直线y=kx+b与直线y=-x平行,
∴k=-1,设此一次函数的解析式为:y=-x+b,
∵直线l1:y=kx+b过点B(5,-1),
∴-1=-5+b,解得:b=4,
∴直线l1的解析式为:y=-x+4;
(2)解方程组
,可得方程组的解:
,
即点A的坐标为(2,2);
由直线l2:y=2x-2可知:C(0,-2),
∴直线AB的解析式为:y=-x+4,
∴直线AB与x轴的交点为D(4,0),
∴由O、A、B、C四点所构成的四边形的面积
=S△AOD+S△BOD+S△OBC
=
OD•2+
OD•1+
OC•5
=
×4×2+
×4×1+
×2×5
=11.
∴k=-1,设此一次函数的解析式为:y=-x+b,
∵直线l1:y=kx+b过点B(5,-1),
∴-1=-5+b,解得:b=4,
∴直线l1的解析式为:y=-x+4;
(2)解方程组
|
|
即点A的坐标为(2,2);
由直线l2:y=2x-2可知:C(0,-2),
∴直线AB的解析式为:y=-x+4,
∴直线AB与x轴的交点为D(4,0),
∴由O、A、B、C四点所构成的四边形的面积
=S△AOD+S△BOD+S△OBC
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=11.

点评:本题考查了两直线平行时系数k的关系,解题的关键是根据函数解析式画出图形,根据图形确定四边形的面积的求解方法.

练习册系列答案
相关题目
将一列有理数-1,2,-3,4,-5,6,…,按如图所示有序排列.根据图中的排列规律可知,“峰1”中峰顶的位置(C的位置)是有理数4,那么,“峰6”中C的位置是有理数 ,2008应排在A、B、C、D、E中 的位置.其中两个填空依次为( )

| A、-28,C |
| B、-31,E |
| C、-30,D |
| D、-29,B |
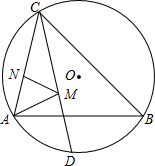 如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M,N分别是线段CD、AC上的动点,则MA+MN的最小值是( )
如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M,N分别是线段CD、AC上的动点,则MA+MN的最小值是( )A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知向量
,
满足|
|=|
|=|
+
|=1,则向量
,
夹角的余弦值为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
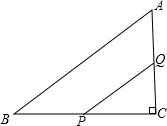 如图,在△ABC中,∠C=90°,BC=8cm,tanB=
如图,在△ABC中,∠C=90°,BC=8cm,tanB=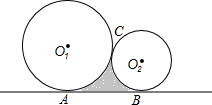 如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.
如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积. 如图,直线y=3x与双曲线y=
如图,直线y=3x与双曲线y=