题目内容
在△ABC和△A1B1C1中,下列命题中真命题的个数为( )
(1)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(2)若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1;
(3)若AB=kA1B1,AC=kA1C1,(k≠0),∠A=∠A1,则△ABC∽△A1B1C1;
(4)若S△ABC=S △A1B1C1,则△ABC∽△A1B1C1.
(1)若∠A=∠A1,∠C=∠C1,则△ABC∽△A1B1C1;
(2)若AC:A1C1=CB:C1B1,∠C=∠C1,则△ABC∽△A1B1C1;
(3)若AB=kA1B1,AC=kA1C1,(k≠0),∠A=∠A1,则△ABC∽△A1B1C1;
(4)若S△ABC=S △A1B1C1,则△ABC∽△A1B1C1.
| A、1 | B、2 | C、3 | D、4 |
考点:相似三角形的判定
专题:
分析:根据相似三角形的性质(①有两角相等的两个三角形相似,②有两边的比相等,并且它们的夹角也相等的两个三角形相似,③有三组对应边的比相等的两三角形相似)逐个判断即可.
解答:解:如图:

∵∠A=∠A1,∠C=∠C1,
∴△ABC∽△A1B1C1,
∴(1)正确;
∵AC:A1C1=CB:C1B1,∠C=∠C1,
∴△ABC∽△A1B1C1,
∴(2)正确;
(3)∵AB=kA1B1,AC=kA1C1,(k≠0),
∴
=
=k,
∵∠A=∠A1,
∴△ABC∽△A1B1C1,
∴(3)正确;
(4)当AB=2,AB边上的高为1,A1B1=1,A1B1边上的高为2时,S△ABC=S △A1B1C1,当△ABC和△A1B1C1不相似,∴(4)错误;
故选C.

∵∠A=∠A1,∠C=∠C1,
∴△ABC∽△A1B1C1,
∴(1)正确;
∵AC:A1C1=CB:C1B1,∠C=∠C1,
∴△ABC∽△A1B1C1,
∴(2)正确;
(3)∵AB=kA1B1,AC=kA1C1,(k≠0),
∴
| AB |
| A1B1 |
| AC |
| A1C1 |
∵∠A=∠A1,
∴△ABC∽△A1B1C1,
∴(3)正确;
(4)当AB=2,AB边上的高为1,A1B1=1,A1B1边上的高为2时,S△ABC=S △A1B1C1,当△ABC和△A1B1C1不相似,∴(4)错误;
故选C.
点评:本题考查了相似三角形的判定的应用,主要考查学生运用定理进行推理的能力,用到的知识点是①有两角相等的两个三角形相似,②有两边的比相等,并且它们的夹角也相等的两个三角形相似,③有三组对应边的比相等的两三角形相似,难度适中.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
下列各组中的两个代数式,不是同类项的是( )
A、2x2y与-
| ||
| B、23与22 | ||
| C、a2b与-5ba2 | ||
| D、x2与32 |
矩形、菱形都具有的性质是( )
| A、对角线相等 |
| B、每一条对角线平分一组对角 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
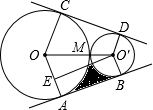 如图,⊙O与⊙O′外切于M,AB、CD分别同时与⊙O、⊙O′都相切的直线,A、B、C、D为切点,O′E⊥OA于E,且∠AOC=120°.若⊙O′的半径为1cm,图中阴影部分的面积是
如图,⊙O与⊙O′外切于M,AB、CD分别同时与⊙O、⊙O′都相切的直线,A、B、C、D为切点,O′E⊥OA于E,且∠AOC=120°.若⊙O′的半径为1cm,图中阴影部分的面积是 直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x,
直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x, 如图,平面直角坐标系内有一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,试求出符合条件的所有动点P的坐标.
如图,平面直角坐标系内有一点A(2,-1),O是原点,P是x轴上一个动点,如果以点P、O、A为顶点的三角形是等腰三角形,试求出符合条件的所有动点P的坐标. 如图,经过原点的直线交双曲线y=-
如图,经过原点的直线交双曲线y=-