题目内容
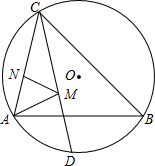 如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M,N分别是线段CD、AC上的动点,则MA+MN的最小值是( )
如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M,N分别是线段CD、AC上的动点,则MA+MN的最小值是( )A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
考点:轴对称-最短路线问题,圆周角定理
专题:
分析:连接OA,OC,过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,则A′N′的长即为MA+MN的最小值.
解答: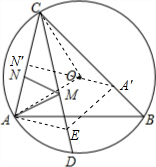 解:连接OA,OC,
解:连接OA,OC,
∵∠ABC=45°,OA=OC=2,
∴∠AOC=90°,
∴AC=
=
=2
.
过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,
∵CD平分∠ACB交⊙O于D,
∴点A与点A′关于直线CD对称,
∴A′N′的长即为MA+MN的最小值,AC=A′C=2
,
∵∠ACB=60°,
∴A′N′=A′C•sin60°=2
×
=
,即MA+MN的最小值是
.
故选B.
 解:连接OA,OC,
解:连接OA,OC,∵∠ABC=45°,OA=OC=2,
∴∠AOC=90°,
∴AC=
| 2OA2 |
| 2×4 |
| 2 |
过点A作AE⊥AC,交CD于点E,过点E作EA′⊥BC于点A′过点A′作A′N′⊥AC于点N′,
∵CD平分∠ACB交⊙O于D,
∴点A与点A′关于直线CD对称,
∴A′N′的长即为MA+MN的最小值,AC=A′C=2
| 2 |
∵∠ACB=60°,
∴A′N′=A′C•sin60°=2
| 2 |
| ||
| 2 |
| 6 |
| 6 |
故选B.
点评:本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
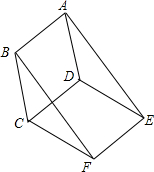 如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )
如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )| A、4个 | B、3个 | C、2个 | D、1个 |
矩形、菱形都具有的性质是( )
| A、对角线相等 |
| B、每一条对角线平分一组对角 |
| C、对角线互相平分 |
| D、对角线互相垂直 |
 直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x,
直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x, 如图,经过原点的直线交双曲线y=-
如图,经过原点的直线交双曲线y=- 实数a,b在数轴上的位置如图所示,化简:|a-
实数a,b在数轴上的位置如图所示,化简:|a- 如图,△ABC中,AM是BC边上的中线,AD⊥BC于D,求证:AB2-AC2=2BC•DM.
如图,△ABC中,AM是BC边上的中线,AD⊥BC于D,求证:AB2-AC2=2BC•DM.