题目内容
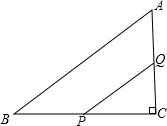 如图,在△ABC中,∠C=90°,BC=8cm,tanB=
如图,在△ABC中,∠C=90°,BC=8cm,tanB=| 3 |
| 4 |
考点:平行线分线段成比例
专题:
分析:如图,首先求出AC=6;证明△ABC∽△QPC,得到
=
,求出λ,即可解决问题.
| CQ |
| CA |
| CP |
| CB |
解答: 解:∵∠C=90°,BC=8,tanB=
解:∵∠C=90°,BC=8,tanB=
,
∴AC=6;设λ秒时PQ∥AB;
∴△ABC∽△QPC,
∴
=
,而CQ=λ,CP=8-2λ,BC=8,AC=6,
∴
=
,
解得:λ=2.4,
∴2.4秒时PQ∥AB.
 解:∵∠C=90°,BC=8,tanB=
解:∵∠C=90°,BC=8,tanB=| 3 |
| 4 |
∴AC=6;设λ秒时PQ∥AB;
∴△ABC∽△QPC,
∴
| CQ |
| CA |
| CP |
| CB |
∴
| λ |
| 6 |
| 8-2λ |
| 8 |
解得:λ=2.4,
∴2.4秒时PQ∥AB.
点评:该题主要考查了平行线分线段成比例定理及其应用问题;正确写出比例式是灵活运用平行线分线段成比例定理的基础和关键.

练习册系列答案
相关题目
在一次女子体操比赛中,八名运动员的年龄(单位:岁)分别为:12,14,12,15,14,14,16,15.这组数据的众数是( )
| A、12 | B、14 | C、15 | D、16 |
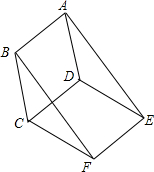 如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )
如图所示,已知?ABCD与?DCFE的周长相等,且∠BAD=60°,∠CFE=110°.则下列结论;①四边形ABFE为平行四边形;②△ADE是等腰三角形;③?ABCD与?DCFE全等;④∠DAE=25°,其中结论正确的个数为( )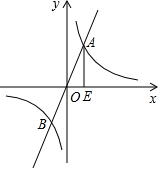 如图,已知函数y=2x图象和函数y=
如图,已知函数y=2x图象和函数y= 直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x,
直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x, 实数a,b在数轴上的位置如图所示,化简:|a-
实数a,b在数轴上的位置如图所示,化简:|a-