题目内容
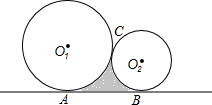 如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.
如图,一台机器的大轮⊙O1和小轮⊙O2外切于点C,且两轮分别和板面相切于A,B两点.若⊙O1的半径为3cm,⊙O2的半径为1cm,求阴影部分面积.考点:相切两圆的性质,扇形面积的计算
专题:
分析:如图,作辅助线;首先求出AD=2,得到O1D=3-1=2;进而得到∠O2O1D=60°,∠O1O2B=120°;求出λ=S扇形O1AC+S扇形O2BC=
+
=
,S梯形ABO2O1=
(1+3)×2
=4
,得到S阴影=4
-λ=4
-
(cm2),即可解决问题.
| 60π•32 |
| 360 |
| 120π•12 |
| 360 |
| 11π |
| 6 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 11π |
| 6 |
解答: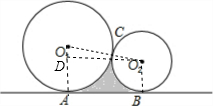 解:如图,连接O1O2,过点O2作O2D⊥AO;
解:如图,连接O1O2,过点O2作O2D⊥AO;
∵⊙O1和⊙O2外切于点C,
且两轮分别和板面相切于A,B两点,
∴O1O2=3+1=4,O1A⊥AB,O2B⊥AB,
∴四边形ABO2D为矩形,
∴AD=O2B=1,O1D=3-1=2,
由勾股定理得:O2D=
=2
;
∴cos∠O2O1D=
=
=
,
∴∠O2O1D=60°,∠O1O2B=120°,
∴λ=S扇形O1AC+S扇形O2BC
=
+
=
,
∴S梯形ABO2O1=
(1+3)×2
=4
,
∴S阴影=4
-
(cm2).
 解:如图,连接O1O2,过点O2作O2D⊥AO;
解:如图,连接O1O2,过点O2作O2D⊥AO;∵⊙O1和⊙O2外切于点C,
且两轮分别和板面相切于A,B两点,
∴O1O2=3+1=4,O1A⊥AB,O2B⊥AB,
∴四边形ABO2D为矩形,
∴AD=O2B=1,O1D=3-1=2,
由勾股定理得:O2D=
| 42-22 |
| 3 |
∴cos∠O2O1D=
| O1D |
| O1O2 |
| 2 |
| 4 |
| 1 |
| 2 |
∴∠O2O1D=60°,∠O1O2B=120°,
∴λ=S扇形O1AC+S扇形O2BC
=
| 60π•32 |
| 360 |
| 120π•12 |
| 360 |
| 11π |
| 6 |
∴S梯形ABO2O1=
| 1 |
| 2 |
| 3 |
| 3 |
∴S阴影=4
| 3 |
| 11π |
| 6 |
点评:该题主要考查了相切两圆的性质、勾股定理、扇形的面积公式等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用相切两圆的性质、勾股定理、扇形的面积公式等几何知识点来分析、解答.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
 如图,已知函数y=2x图象和函数y=
如图,已知函数y=2x图象和函数y= 直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x,
直线L1:y=kx+b过点B(5,-1)且平行于直线y=-x, 如图,l1∥l2∥l3,DE=6,EF=9,AB=4,则AC=
如图,l1∥l2∥l3,DE=6,EF=9,AB=4,则AC=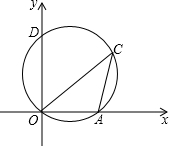 已知:如图,点D的坐标为(0,6),过原点O,D点的圆交x轴的正半轴于A点.圆周角∠OCA=30°,则A点的坐标为
已知:如图,点D的坐标为(0,6),过原点O,D点的圆交x轴的正半轴于A点.圆周角∠OCA=30°,则A点的坐标为