题目内容
9.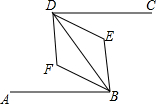 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )| A. | ∠ABE=2∠CDE | B. | ∠ABE=3∠CDE | C. | ∠ABE=∠CDE+90° | D. | ∠ABE+∠CDE=180° |
分析 延长BF与CD相交于M,根据两直线平行,同位角相等可得∠M=∠CDE,再根据两直线平行,内错角相等可得∠M=∠ABF,从而求出∠CDE=∠ABF,再根据角平分线的定义解答.
解答  解:延长BF与CD相交于M,
解:延长BF与CD相交于M,
∵BF∥DE,
∴∠M=∠CDE,
∵AB∥CD,
∴∠M=∠ABF,
∴∠CDE=∠ABF,
∵BF平分∠ABE,
∴∠ABE=2∠ABF,
∴∠ABE=2∠CDE.
故选A.
点评 本题考查了平行线的性质,角平分线的定义,作辅助线,是利用平行线的性质的关键,也是本题的难点.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
14.下列说法正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角互补的平行四边形是矩形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 菱形是轴对称图形,它的对角线就是它的对称轴 |
18.若关于x的分式方程$\frac{x}{x-2}$-2m=$\frac{3m}{x-2}$无解,则m的值为( )
| A. | m=$\frac{2}{3}$ | B. | m=$\frac{2}{3}$或m=2 | C. | m=$\frac{1}{2}$ | D. | m=$\frac{2}{3}$或m=$\frac{1}{2}$ |
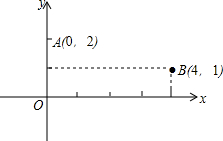 已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.
已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.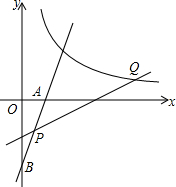 如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.
如图,直线l:y=kx-2k交坐标轴于A,B两点,点P(m,n)为直线l上的一点,且满足关系式2m2+2n2-4m+8n+10=0.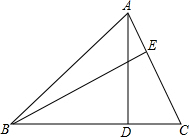 如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE=$\frac{24}{5}$cm.
如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE=$\frac{24}{5}$cm.