题目内容
12.7a($\sqrt{8a}$-$\sqrt{2a}$)-2a2$\sqrt{\frac{1}{2a}}$(a>0)分析 根据二次根式的性质化简,再进行化简即可解答.
解答 解:原式=7a(2$\sqrt{2a}-\sqrt{2a}$)-$2{a}^{2}•\frac{\sqrt{2a}}{2a}$
=7a$•\sqrt{2a}$-a$\sqrt{2a}$
=6a$\sqrt{2a}$.
点评 本题考查二次根式的加减法,解决本题的关键是先进行化简.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
20.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{{x}^{2}}$ | B. | $\frac{x}{\sqrt{3}}$ | C. | $\sqrt{8}$ | D. | $\frac{\sqrt{2x}}{2}$ |
7.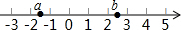 实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
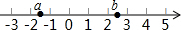 实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )
实数a、b在数轴上的位置如图,则化简$\sqrt{{a}^{2}}$+$\sqrt{{b}^{2}}$-$\sqrt{(a-b)^{2}}$的结果是( )| A. | 0 | B. | -2a | C. | 2b | D. | -2a+2b |
4.单项式-$\frac{2x{y}^{2}}{5}$的系数和次数分别是( )
| A. | $\frac{2}{5}$,3 | B. | -$\frac{2}{5}$,2 | C. | -2,3 | D. | -$\frac{2}{5}$,3 |
9.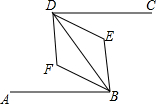 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )| A. | ∠ABE=2∠CDE | B. | ∠ABE=3∠CDE | C. | ∠ABE=∠CDE+90° | D. | ∠ABE+∠CDE=180° |
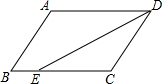 如图,在?ABCD中,已知AD=10cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE=4cm.
如图,在?ABCD中,已知AD=10cm,AB=6cm,DE平分∠ADC交BC边于点E,则BE=4cm.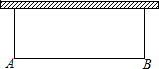 如图中有一面围墙(可利用的最大长度为100m),现打算沿围墙围成一个面积为120m2的长方形花圃.设花圃的一边AB=xm,另一边为ym,求y关于x的函数表达式,并指出其中自变量的取值范围.
如图中有一面围墙(可利用的最大长度为100m),现打算沿围墙围成一个面积为120m2的长方形花圃.设花圃的一边AB=xm,另一边为ym,求y关于x的函数表达式,并指出其中自变量的取值范围.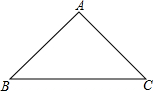 在△ABC中,AB=AC,∠BAC=90°,若点D、E在边BC上,∠DAE=45°,BE=CD=4,求AC的长.
在△ABC中,AB=AC,∠BAC=90°,若点D、E在边BC上,∠DAE=45°,BE=CD=4,求AC的长.