题目内容
1.大家知道$\sqrt{5}$是无理数.而无理数是无限不循环小数,因此$\sqrt{5}$的小数部分我们不可能全部地写出来,我们可以写出它的整数部分,然后再表示小数部分,因为4<5<9,所以2<$\sqrt{5}$<3,所以其整数部分是2,小数部分是$\sqrt{5}$-2.已知9+$\sqrt{13}$与9-$\sqrt{13}$的小数部分分别是a和b,求a+b的相反数的立方根.分析 根据3<$\sqrt{13}$<4,可得$\sqrt{13}$的大小,根据已知得出a、b 的值,再进一步求a+b的相反数的立方根可得答案.
解答 解:∵3<$\sqrt{13}$<4,
∴9+$\sqrt{13}$的小数部分为a=9+$\sqrt{13}$-12=$\sqrt{13}$-3;
9-$\sqrt{13}$的小数部分为b=9-$\sqrt{13}$-5=4-$\sqrt{13}$;
所以a+b=$\sqrt{13}$-3+4-$\sqrt{13}$=1;
1的相反数是-1,-1的立方根为-1.
∴a+b的相反数的立方根是-1.
点评 此题考查估算无理数的大小,估算出$\sqrt{13}$的大小是解决问题的关键.

练习册系列答案
相关题目
11.下列长度的线段能组成一个三角形的是( )
| A. | 15cm、10cm、7cm | B. | 4cm、5cm、10cm | C. | 3cm、8cm、5cm | D. | 3cm、3cm、6cm |
13.己知方程2xa+b-xa-b-ab=0是关于x的一元二次方程,则对应a、b的值有( )
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
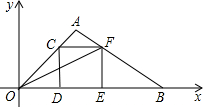 在直角坐标系中,O为坐标原点,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是($\frac{3}{2}$,0)(3,0).
在直角坐标系中,O为坐标原点,点A的坐标为(1,1),点C是线段OA上的一个动点(不运动至O,A两点),过点C作CD⊥x轴,垂足为D,以CD为边在右侧作正方形CDEF.连接AF并延长交x轴的正半轴于点B,连接OF,若以B,E,F为顶点的三角形与△OFE相似,B点的坐标是($\frac{3}{2}$,0)(3,0).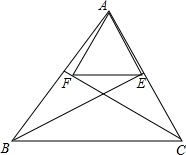 如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC.
如图,过△ABC的顶点A向∠ABC和∠ACB的平分线作垂线,其垂足分别为E,F,求证:EF∥BC. 如图,△ABD与△ACE都是等腰直角三角形,∠BAD=∠CAE=90°.
如图,△ABD与△ACE都是等腰直角三角形,∠BAD=∠CAE=90°.