题目内容
13. 如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为14.
如图,在直角三角形ABC中,∠ACB=90°,点O在AB上,且CA=CO,若将直角三角形ABC绕着点A顺时针旋转,得到直角三角形AED,B、C的对应点分别为E、D,且点D落在CO的延长线上,连接BE交CO的延长线于点F,若CA=6,AB=18,则BF的长为14.
分析 根据旋转的性质可得AC=AD,AB=AE,∠CAD=∠BAE,再根据等腰三角形两底角相等求出∠ACD=∠ABE,从而得到△AOC∽△FOB,根据相似三角形对应边成比例求出BF=OB,过点C作CH⊥AB于H,根据等腰三角形三线合一的性质可得AO=2AH,再由△ACH∽△ABC求出AH,然后根据BO=AB-AO即可得解.
解答 解:∵△ABC以点A为旋转中心顺时针旋转得到△ADE,
∴AC=AD,AB=AE,∠CAD=∠BAE(为旋转角),
∵∠ACD=$\frac{1}{2}$(180°-∠CAD),∠ABE=$\frac{1}{2}$(180°-∠BAE),
∴∠ACD=∠ABE,
又∵∠AOC=∠BOF,
∴△AOC∽△FOB,
∴$\frac{AC}{OC}=\frac{FB}{OB}$,
∵AC=OC,
∴BF=OB,
过点C作CH⊥AB于H,则AO=2AH,
∵△ACH∽△ABC,
∴AC2=AH•AB,
∴62=18•AH,
∴AH=2,
∴AO=4,
∴BF=BO=AB-AO=18-4=14.
点评 本题考查了旋转的性质,等腰三角形两底角相等的性质,等腰三角形三线合一的性质,利用三角形相似求出BF=OB是解题的关键,也是本题的难点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.某校初一年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5;2,请结合图中相关数据回答下列问题:

(1)求出样本容量,并补全直方图(在图中标出各组人数);
(2)课堂发言次数的中位数落在哪个组;
(3)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数.

(1)求出样本容量,并补全直方图(在图中标出各组人数);
(2)课堂发言次数的中位数落在哪个组;
(3)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数.
| 组别 | 课堂发言次数n |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
3.如果一个多边形的内角和等于720度,那么这个多边形的边数为( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
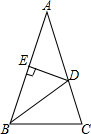 如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.
如图,在△ABC中,AB=AC,∠A=36°,BD为角平分线,DE⊥AB,垂足为E.