题目内容
3．如果一个多边形的内角和等于720度，那么这个多边形的边数为（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
分析 n边形的内角和可以表示成（n-2）•180°，设这个正多边形的边数是n，就得到方程，从而求出边数．
解答 解：这个正多边形的边数是n，则
（n-2）•180°=720°，
解得：n=6．
则这个正多边形的边数是6．
故选：C．
点评 考查了多边形内角和定理，此题比较简单，只要结合多边形的内角和公式，寻求等量关系，构建方程求解．
练习册系列答案
天天练口算系列答案
相关题目
如图，在直角三角形ABC中，∠ACB=90°，点O在AB上，且CA=CO，若将直角三角形ABC绕着点A顺时针旋转，得到直角三角形AED，B、C的对应点分别为E、D，且点D落在CO的延长线上，连接BE交CO的延长线于点F，若CA=6，AB=18，则BF的长为14．
11．掷一个质地均匀的正方体骰子，当骰子停止后，朝上一面的点数为3的概率是（ ）
| A． | 1 | B． | $\frac{1}{5}$ | C． | $\frac{1}{6}$ | D． | 0 |
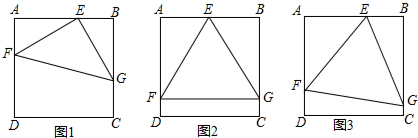
8．
在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（ ）
在平面直角坐标系中，矩形OABC如图所示．点A在x轴正半轴上，点C在y轴正半轴上，且OA=6，OC=4，D为OC中点，点E、F在线段OA上，点E在点F左侧，EF=3．当四边形BDEF的周长最小时，点E的坐标是（ ）| A． | （$\frac{1}{2}$，0） | B． | （1，0） | C． | （$\frac{3}{2}$，0） | D． | （2，0） |
15．
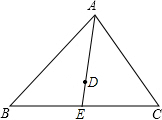如图，△ABC中，D是△ABC的重心，连接AD并延长，交BC于点E，若BC=6，则EC=（ ）
如图，△ABC中，D是△ABC的重心，连接AD并延长，交BC于点E，若BC=6，则EC=（ ）| A． | 2 | B． | 2.5 | C． | 3 | D． | 3.5 |
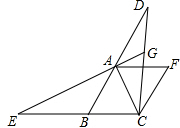如图，在菱形ABCF中，∠ABC=60°，延长BA至点D，延长CB至点E，使BE=AD，连结CD，EA，延长EA交CD于点G．