题目内容
如图,已知A(a,b),AB⊥y轴于B,且满足|a-2|+(b-2)2=0,
(1)求A点坐标;
(2)如图1,分别以AB,AO为边作等边三角形△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由;
(3)如图2,过A作AE⊥x轴于E,点F、G分别为线段OE、AE上的两个动点,满足∠FBG=45°,试探究
的值是否发生变化?如果不变,求其值;如果变化,请说明理由.
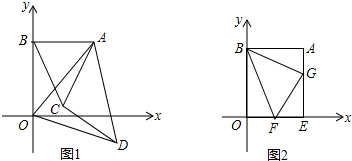
(1)求A点坐标;
(2)如图1,分别以AB,AO为边作等边三角形△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由;
(3)如图2,过A作AE⊥x轴于E,点F、G分别为线段OE、AE上的两个动点,满足∠FBG=45°,试探究
| OF+AG |
| FG |
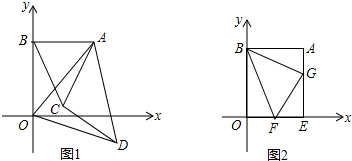
考点:全等三角形的判定与性质,非负数的性质:绝对值,非负数的性质:偶次方,坐标与图形性质,等边三角形的性质
专题:
分析:(1)根据|a-2|+(b-2)2=0得出|a-2|=(b-2)2=0,求出即可;
(2)根据等边三角形的性质得出AB=AC,AO=AD,∠BAC=∠OAD=60°,求出∠BAO=∠CAD,证出△BAO≌△CAD即可;
(3)在FO的延长线上截取OM=AG,连接BM,证出△BOM≌△BAG,推出∠ABG=∠MBO,BG=BM,求出∠MBF=∠FBG=45°,证出△MBF≌△GBF,推出FM=FG即可.
(2)根据等边三角形的性质得出AB=AC,AO=AD,∠BAC=∠OAD=60°,求出∠BAO=∠CAD,证出△BAO≌△CAD即可;
(3)在FO的延长线上截取OM=AG,连接BM,证出△BOM≌△BAG,推出∠ABG=∠MBO,BG=BM,求出∠MBF=∠FBG=45°,证出△MBF≌△GBF,推出FM=FG即可.
解答:解:(1)∵|a-2|+(b-2)2=0,|a-2|≥0,(b-2)2≥0,
∴|a-2|=(b-2)2=0,
∴a=b=2,
∴点A坐标为(2,2);
(2)∵△ABC、△AOD均为等边三角形,
∴AB=AC,AO=AD,∠BAC=∠OAD=60°,
∵∠BAO+∠CAO=∠BAC,∠CAD+∠CAO=∠OAD,
∴∠BAO=∠CAD,
∵在△BAO和△CAD中,
,
∴△BAO≌△CAD,(SAS)
∴CD=OB=2,∠ACD=∠ABO=90°,
∴AC=CD,AC⊥CD;
(3)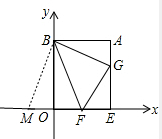
如图,在FO的延长线上截取OM=AG,连接BM,
∵AB⊥y轴,AE⊥x轴,x轴⊥y轴,A(2,2),
∴∠ABO=∠AEO=∠BOE=90°,AB=AE=2,
∵∠A=∠BOM=90°,
在△BOM和△BAG中
∴△BOM≌△BAG,
∠ABG=∠MBO,BG=BM,
∵∠FBG=45°,∠ABO=90°,
∴∠ABG+∠OBF=45°,
∴∠MBO+∠OBF=45°,
∴∠MBF=∠FBG=45°,
在△MBF和△GBF中
∴△MBF≌△GBF,
∴FM=FG,
∵AG=OM,
∴OF+AG=FG,
∴
的值是1,
即
的值不发生变化,其值是1.
∴|a-2|=(b-2)2=0,
∴a=b=2,
∴点A坐标为(2,2);
(2)∵△ABC、△AOD均为等边三角形,
∴AB=AC,AO=AD,∠BAC=∠OAD=60°,
∵∠BAO+∠CAO=∠BAC,∠CAD+∠CAO=∠OAD,
∴∠BAO=∠CAD,
∵在△BAO和△CAD中,
|
∴△BAO≌△CAD,(SAS)
∴CD=OB=2,∠ACD=∠ABO=90°,
∴AC=CD,AC⊥CD;
(3)

如图,在FO的延长线上截取OM=AG,连接BM,
∵AB⊥y轴,AE⊥x轴,x轴⊥y轴,A(2,2),
∴∠ABO=∠AEO=∠BOE=90°,AB=AE=2,
∵∠A=∠BOM=90°,
在△BOM和△BAG中
|
∴△BOM≌△BAG,
∠ABG=∠MBO,BG=BM,
∵∠FBG=45°,∠ABO=90°,
∴∠ABG+∠OBF=45°,
∴∠MBO+∠OBF=45°,
∴∠MBF=∠FBG=45°,
在△MBF和△GBF中
|
∴△MBF≌△GBF,
∴FM=FG,
∵AG=OM,
∴OF+AG=FG,
∴
| OF+AG |
| FG |
即
| OF+AG |
| FG |
点评:本题考查了等边三角形的性质,全等三角形的性质和判定,坐标与图形性质等知识点的应用,能综合运用性质进行推理和计算是解此题的关键,有一定的难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若⊙O的面积为25π,在同一平面内有一个点P,且点P到圆心O的距离为4.9,则点P与⊙O的位置关系为( )
| A、点P在⊙O外 |
| B、点P在⊙O上 |
| C、点P在⊙O内 |
| D、无法确定 |
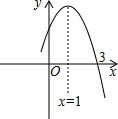 若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )
若y=ax2+bx+c的部分图象如图所示,则关于x的方程ax2+bx+c=0的另一个解为( )| A、-2 | B、-1 | C、0 | D、1 |
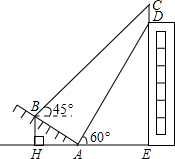 如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1:
如图,某大楼的顶部竖有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底仰角为60°,沿坡度为1: 如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.
如图,AB⊥BD,ED⊥BD,C是BD上的一点,BC=DE,AB=CD.求证:AC⊥CE.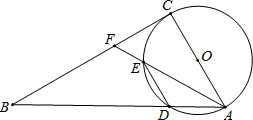 如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC.
如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC. 如图,点E在DF上,点B在AC上,BD∥CE,∠C=∠D,∠A与∠F相等吗?为什么?
如图,点E在DF上,点B在AC上,BD∥CE,∠C=∠D,∠A与∠F相等吗?为什么?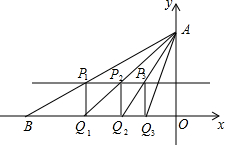 已知直角坐标系中,点A(0,3),B(-6,0).连结AB,作直线y=1,交AB于点P1,过P1作P1Q1⊥x轴于Q1;连结AQ1,交直线y=1于点P2,P2Q2⊥x轴于Q2;…以此类推.则点Q3的坐标为
已知直角坐标系中,点A(0,3),B(-6,0).连结AB,作直线y=1,交AB于点P1,过P1作P1Q1⊥x轴于Q1;连结AQ1,交直线y=1于点P2,P2Q2⊥x轴于Q2;…以此类推.则点Q3的坐标为