题目内容
若实数x、y满足等式：x+y=xy，则称这两个数为一对“和谐数”．请写出一对这样的“和谐数” ．
考点：实数
专题：新定义
分析：实数x、y满足等式：x+y=xy，当x=2时，代入得到2+y=2y，求出y即可．
解答：解：∵实数x、y满足等式：x+y=xy，
当x=2时，代入得：2+y=2y，
∴y=2，
故2、2是一对“和谐数”．
故答案是：2和2．
当x=2时，代入得：2+y=2y，
∴y=2，
故2、2是一对“和谐数”．
故答案是：2和2．
点评：本题考查了和谐数的性质及等式求解，解题的关键是理解新定义运算的法则和“和谐数”的定义．
练习册系列答案
相关题目
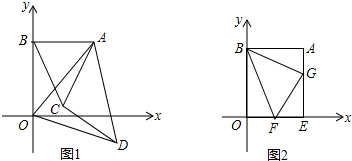
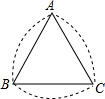如图所示的曲边三角形可按下述方法作出：作等边三角形ABC；分别以点A，B，C为圆心，以AB的长为半径作
如图所示，AB是⊙O的直径，C、D在⊙O上，OC∥BD，求证：AC=CD．
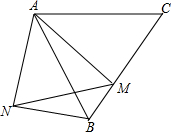如图，M是等边△ABC的边BC上一点，以AM为一边向外作等边△AMN，连接NB，请找出图中的一组全等三角形，并进行证明．
已知：如图O是△ABC内一点，且∠OBC=
已知，如图，△ABC的坐标分别是A（0，-2）、B（2，-4）、C（4，-1）．