题目内容
5. 已知,如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm
已知,如图所示,折叠矩形的一边AD,使点D落在BC边的点F处,如果AB=8cm,BC=10cm(1)求FC的长;
(2)求EC的长.
分析 (1)根据折叠的性质得AF=AD=10,DE=EF,在Rt△ABF中,利用勾股定理计算出BF=6,则FC=4;
(2)设EC=x,则DE=EF=8-x,在Rt△EFC中,根据勾股定理得x2+42=(8-x)2,然后解方程即可.
解答 解:(1)∵四边形ABCD为矩形,
∴DC=AB=8,AD=BC=10,∠B=∠D=∠C=90°,
∵折叠矩形的一边AD,使点D落在BC边的点F处
∴AF=AD=10,DE=EF,
在Rt△ABF中,BF=BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴FC=BC-BF=4;
(2)设EC=x,则DE=8-x,EF=8-x,
在Rt△EFC中,
∵EC2+FC2=EF2,
∴x2+42=(8-x)2,
解得x=3
∴EC的长为3.
点评 本题主要考查了折叠变换问题,解决本题的关键是结合图形根据翻折的性质得到一些相等的线段,然后灵活运用勾股定理进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列各数组中,不能作为直角三角形三边长的是( )
| A. | 9,12,15 | B. | 5,6,7 | C. | 6,8,10 | D. | 7,24,25 |
15.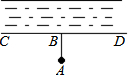 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
 如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )
如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是( )| A. | 两点之间线段最短 | B. | 点到直线的距离 | ||
| C. | 两点确定一条直线 | D. | 垂线段最短 |
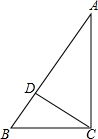 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$