题目内容
20.已知,如图,在△ABC中,∠ABC=90°,BD⊥AC于D,CE平分∠BCA,交AB于G,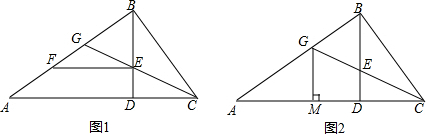
(1)如图1,作EF∥AC,交AB于F.求证:BE=AF;
(2)如图2,过G作GM⊥AC,垂足为M,连结ME,判断四边形BGME的形状并证明.
分析 (1)分别过E、F作EH⊥BC,FI⊥AB,垂足分别为H、I,由条件证明△AFI≌△CEH即可;
(2)首先根据角平分线的性质得到GB=GM,∠BGC=∠MGC,然后根据GM⊥AC,BD⊥AC于得到GM∥BD,从而得到∠GEB=∠BGE,进一步得到GM=BE,从而判定四边形四边形BGME是菱形.
解答 证明:(1)分别过E、F作EH⊥BC,FI⊥AC,垂足分别为H、I,如图1,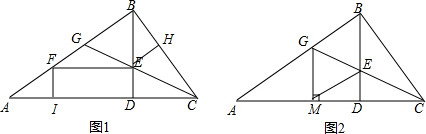
∵BD⊥AC于D,EF∥AC,
∴四边形DEFI为矩形,
∴FI=ED,
∵CE平分∠ACB,
∴ED=EH,
∴FI=EH,
∵∠ABC=90°,
∴∠DBH+∠ABD=90°,
且∠A+∠ABD=90°,
∴∠FAI=∠ECH,
在△AFI和△BEH中,
$\left\{\begin{array}{l}{∠FAI=∠EBH}\\{∠AIF=∠EHB=90°}\\{FI=EH}\end{array}\right.$,
∴△AFI≌△BEH(AAS),
∴AF=BE;
(2)∵CE平分∠BCA,∠GMC=∠GBC=90°,如图2,
∴GB=GM,∠BGC=∠MGC,
∵GM⊥AC,BD⊥AC于D,
∴GM∥BD,
∴∠MGE=∠GEB
∴∠GEB=∠BGE,
∴GB=BE,
∴GM=BE,
∴四边形BGME菱形.
点评 本题考查了菱形的判定及角平分线的性质,解题的关键是利用角平分线的性质得到GM=BE,这为判定菱形提供了必要的条件.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
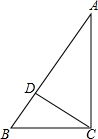 如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$
如图,CD是AB上的高,AC=4,BC=3,DB=$\frac{9}{5}$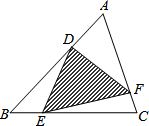 如图,△ABC中,点D在AB上,AD=$\frac{1}{3}$AB.点E在BC上,BE=$\frac{1}{4}$BC.点F在AC上,CF=$\frac{1}{5}$CA.已知阴影部分(即△DEF)的面积是25cm2,则△ABC的面积为60 cm2.(写出简要推理)
如图,△ABC中,点D在AB上,AD=$\frac{1}{3}$AB.点E在BC上,BE=$\frac{1}{4}$BC.点F在AC上,CF=$\frac{1}{5}$CA.已知阴影部分(即△DEF)的面积是25cm2,则△ABC的面积为60 cm2.(写出简要推理)