题目内容
13.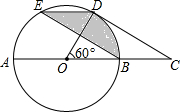 如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB.
如图,在⊙O中,AB是直径,点D是⊙O上一点且∠BOD=60°,过点D作⊙O的切线CD交AB的延长线于点C,E为$\widehat{AD}$的中点,连接DE,EB.(1)求证:四边形BCDE是平行四边形;
(2)已知图中阴影部分面积为12π,求⊙O的半径r.
分析 (1)由∠BOD=60°得到E为$\widehat{AD}$的中点,得到$\widehat{AE}$,于是得到DE∥BC,根据CD是⊙O的切线,得到OD⊥CD,于是得到BE∥CD,即可证得四边形BCDE是平行四边形;
(2)连接OE,由(1)知,$\widehat{AE}$,得到∠BOE=120°,根据扇形的面积公式列方程即可得到结论.
解答 解:(1)∵CD是⊙O的切线,∴∠CDO=90°,∵∠BOD=60°,
∴∠C=30°,∠AOD=120°,
∵E为 $\widehat{AD}$的中点,
∴∠AOE=∠DOE=60°,
∴∠BOE=120°,
∵OE=OB,
∴∠OEB=∠OBE=30°,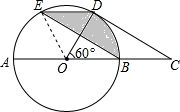
∴∠C=∠OBE=∠E,
∴DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形;
(2)连接OE,由(1)知,$\widehat{AE}$=$\widehat{DE}$=$\widehat{BD}$,
∴∠BOE=120°,
∵阴影部分面积为6π,
∴$\frac{60•π•{r}^{2}}{360}$=12π,
∴r=6$\sqrt{2}$.
点评 本题考查了切线的性质,平行四边形的判定,扇形的面积公式,垂径定理,证明$\widehat{AE}$=$\widehat{DE}$=$\widehat{BD}$是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
3.已知一个直角三角形的两直角边之和是20cm,则这个直角三角形面积的最大值是( )cm2.
| A. | 25 | B. | 50 | C. | 75 | D. | 不确定 |
 如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使∠BAC=90°,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为24m.
如图,为测量小区内池塘最宽处A、B两点间的距离,在池塘边定一点C,使∠BAC=90°,并测得AC的长18m,BC的长为30m,则最宽处AB的距离为24m.