题目内容
18.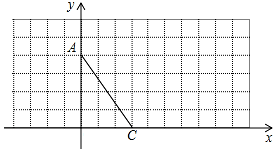 如图,在直角坐标系中,A(0,4)、C(3,0),
如图,在直角坐标系中,A(0,4)、C(3,0),(1)①画出线段AC关于y轴对称线段AB,B点的坐标为(-3,0);
②将线段CA绕点C顺时针旋转一个角,得到对应线段CD,使得AD∥x轴,请画出线段CD;
(2)若直线y=kx平分(1)中四边形ABCD的面积,实数k的值为$\frac{4}{3}$.
分析 (1)①根据关于y轴对称的点的横坐标互为相反数确定出点B的位置,然后连接AB即可;②根据轴对称的性质找出点A关于直线x=3的对称点,即为所求的点D;
(2)对边平行且相等的四边形是平行四边形即可判定四边形ABCD的形状,根据平行四边形的性质,平分四边形面积的直线经过中心,然后求出AC的中点,代入直线计算即可求出k值.
解答 解:(1)①如图,线段AB即为所求线段,点B的坐标为(-3,0),
故答案为:(-3,0);
②如图,线段CD即为所求线段;
(2)由(1)知四边形ABCD是平行四边形,
∵直线y=kx平分(1)中四边形ABCD的面积,
则直线y=kx必过对角线的交点E,
∵点E坐标为为($\frac{3}{2}$,2),
∴k=$\frac{2}{\frac{3}{2}}$=$\frac{4}{3}$,
故答案为:$\frac{4}{3}$.
点评 本题考查了利用旋转变换作图,利用轴对称变换作图,还考查了平行四边形的判定与性质,是基础题,要注意平分四边形面积的直线经过中心的应用.

练习册系列答案
相关题目
9.下列语句不是命题的为( )
| A. | 同角的余角相等 | B. | 两条直线相交,只有一个交点 | ||
| C. | 若a-c=b-c,则a=b | D. | 作直线AB的垂线 |
3.已知一个直角三角形的两直角边之和是20cm,则这个直角三角形面积的最大值是( )cm2.
| A. | 25 | B. | 50 | C. | 75 | D. | 不确定 |
 如图,已知△ABC,利用尺规作出一个新三角形,使新三角形与△ABC对应线段比为2:1(不写作法,保留作图痕迹).
如图,已知△ABC,利用尺规作出一个新三角形,使新三角形与△ABC对应线段比为2:1(不写作法,保留作图痕迹).