题目内容
18.求m的取值范围,使关于x的方程x2+2(m-1)x+2m+6=0;(1)有一正一负两个根;
(2)有两个实根,其中一个根大于1,另一个根小于1;
(3)有两个实根,其中一个根大于4,另一个根小于1;
(4)有两个相异根且都大于1.
分析 (1)有一正一负两个根时,△>0,且两根之积<0;
(2)有两个实根时,△≥0,且(x1-1)(x2-1)<0,据此列出方程组并解答即可;
(3)依题意得到:△≥0,且f(1)<0且f(4)>0,据此列出方程组并解答即可;
(4)有两个相异根且都大于1时,△>0,且f(1)>0、两根之积>1,两根之和>2.
解答 解:(1)依题意得:$\left\{\begin{array}{l}{△=4(m-1)^{2}-4(2m+6)>0}\\{2m+6<0}\end{array}\right.$,
解得m<-3;
(2)依题意得:$\left\{\begin{array}{l}{△=4(m-1)^{2}-4(2m+6)≥0}\\{({x}_{1}-1)({x}_{2}-1)<0}\end{array}\right.$,
整理,得
$\left\{\begin{array}{l}{(m-5)(m+1)≥0}\\{4m+5<0}\end{array}\right.$,
解得m<-$\frac{5}{4}$;
(3)依题意得:$\left\{\begin{array}{l}{△=4(m-1)^{2}-4(2m+6)≥0}\\{1+2(m-1)+2m+6<0}\\{16+8(m-1)+2m+6>0}\end{array}\right.$,
解得-$\frac{7}{5}$<m<-$\frac{5}{4}$;
(4)依题意得:$\left\{\begin{array}{l}{△=4(m-1)^{2}-4(2m+6)>0}\\{1+2(m-1)+2m+6>0}\\{2(1-m)>2}\\{2m+6>1}\end{array}\right.$,
解得-$\frac{5}{2}$<m<-$\frac{5}{4}$.
点评 本题考查了一元二次方程根的分布,其中根据已知结合一元二次方程根的个数与△的关系和韦达定理,构造关于m的不等式是解答的关键.

| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | y=$\frac{x}{5}$ | B. | y=$\frac{2}{x}$ | C. | y=x2-2x-1 | D. | y=8x-4 |

| A. | 48π | B. | 50π | C. | 58π | D. | 60π |
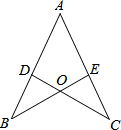 如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.
如图所示,在△ABC中,AB=AC,D、E是AB、AC的中点,求证:△ABE≌△ACD.