题目内容
 已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE=∠ACD,BE、CD交于点G.
已知:如图,在△ABC中,点D、E分别在边AB、AC上,且∠ABE=∠ACD,BE、CD交于点G.(1)求证:△AED∽△ABC;
(2)如果BE平分∠ABC,求证:DE=CE.
考点:相似三角形的判定与性质
专题:证明题
分析:(1)证明B、C、E、D四点共圆,得到∠ADE=∠ACB,即可解决问题.
(2)如图,作辅助线,证明EM=EF;由sinα=
,sinα=
,得到
=
,根据ME=EF,即可解决问题.
(2)如图,作辅助线,证明EM=EF;由sinα=
| ME |
| DE |
| EF |
| EC |
| ME |
| DE |
| EF |
| EC |
解答: (1)证明:∵∠ABE=∠ACD,
(1)证明:∵∠ABE=∠ACD,
∴B、C、E、D四点共圆,
∴∠ADE=∠ACB,而∠A=∠A,
∴△AED∽△ABC.
(2)解:过点E作EM⊥AB,EF⊥BC;
∵BE平分∠ABC,
∴EM=EF;设∠ADE=∠ACB=α,
则sinα=
,sinα=
,
∴
=
,而ME=EF,
∴DE=CE.
 (1)证明:∵∠ABE=∠ACD,
(1)证明:∵∠ABE=∠ACD,∴B、C、E、D四点共圆,
∴∠ADE=∠ACB,而∠A=∠A,
∴△AED∽△ABC.
(2)解:过点E作EM⊥AB,EF⊥BC;
∵BE平分∠ABC,
∴EM=EF;设∠ADE=∠ACB=α,
则sinα=
| ME |
| DE |
| EF |
| EC |
∴
| ME |
| DE |
| EF |
| EC |
∴DE=CE.
点评:该题主要考查了相似三角形的判定及其性质的应用问题;应牢固掌握相似三角形的判定及其性质、四点共圆的判定等几何知识点.

练习册系列答案
相关题目
⊙O的半径为3,圆心O到直线l的距离是4,则⊙O与直线l的关系是( )
| A、相交 | B、相切 |
| C、相离 | D、相交或相切 |
 已知平面上四点A、B、C、D,如图:(1)画直线AB;(2)画射线AD;(3)直线AB、CD相交于E;(4)连接AC、BD相交于点F.(5)延长AC至M,使CM等于2AC.
已知平面上四点A、B、C、D,如图:(1)画直线AB;(2)画射线AD;(3)直线AB、CD相交于E;(4)连接AC、BD相交于点F.(5)延长AC至M,使CM等于2AC. 如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点. 甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有6个;其中正确的结论有
如图,OA⊥OC,OB⊥OD,4位同学观察图形后分别说了自己的观点. 甲:∠AOB=∠COD;乙:∠BOC+∠AOD=180°;丙:∠AOB+∠COD=90°;丁:图中小于平角的角有6个;其中正确的结论有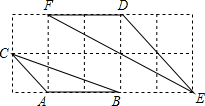 如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△DEF:S△ABC的值为
如图,如果△ABC与△DEF都是正方形网格中的格点三角形(顶点在格点上),那么S△DEF:S△ABC的值为 如图,P为?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PAD.你发现其中两个不相等的三角形的面积之和与平行四边形ABCD面积之间有什么关系?从而你能得到什么结论?证明你的结论.
如图,P为?ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PAD.你发现其中两个不相等的三角形的面积之和与平行四边形ABCD面积之间有什么关系?从而你能得到什么结论?证明你的结论. 已知直线L1:y=
已知直线L1:y= 如图所示,△ABC中,∠BAC=110°,点D,E,F分别在线段AB、BC、AC上,且BD=BE,CE=CF,求∠DEF的度数.
如图所示,△ABC中,∠BAC=110°,点D,E,F分别在线段AB、BC、AC上,且BD=BE,CE=CF,求∠DEF的度数.