题目内容

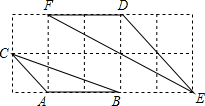如图，如果△ABC与△DEF都是正方形网格中的格点三角形（顶点在格点上），那么S△DEF：S△ABC的值为
 
．
考点：相似三角形的判定与性质
专题：网格型
分析：如图，设正方形网格的边长为1，根据勾股定理求出△EFD、△ABC的边长，运用三边对应成比例，则两个三角形相似这一判定定理证明△EDF∽△BAC，即可解决问题．
解答：解：如图，设正方形网格的边长为1，由勾股定理得：
DE2=22+22，EF2=22+42，
∴DE=2
2
，EF=2
5
；
同理可求：AC=
2
，BC=
10
，
∵DF=2，AB=2，
∴
EF
BC
=
DE
AB
=
DF
AC
=
2
，
∴△EDF∽△BAC，
∴S△DEF：S△ABC=DF2：AC2=2，
故答案为2．
点评：该题主要考查了相似三角形的判定及其性质定理的应用问题；应牢固掌握有关定理，这是灵活运用解题的关键；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
李强同学用棱长为1的正方体在桌面上堆成如图所示的图形，然后把露出的表面都染成红色，则表面被他染成红色的面积为
 
．
如图，在平面直角坐标系xOy中，A（-1，5），B（-1，0），C（-4，3）．
（1）求出△ABC的面积．
（2）作出△ABC向下平移1个单位，再向左平移2个单位后的图形△A2B2C2．
（3）作出△ABC以A为旋转中心逆时针旋转90°后的图形△A3B3C3．
一张长方形纸片，剪下一个正方形，剩下一个长方形，称为第一次操作；在剩下的长方形纸片中再剪下一个正方形，剩下一个长方形，称为第二次操作；…；若在第n次操作后，剩下的图形为正方形，则称原图形为n阶奇异长方形．如图1，长方形ABCD中，若AB=2，BC=6，则称形ABCD为2阶奇异长方形．如图2，长方形ABCD中，若AB=2，BC=8，则称形ABCD为3阶奇异长方形．

（1）判断与操作：
如图3，长方形ABCD长为5，宽为2，它是奇异长方形吗？如果是，请写出它是几阶奇异长方形，并在图中画出裁剪线，并标出数据；如果不是，请说明理由．
（2）探究与计算：
已知长方形ABCD的一边长为20，另一边长为a（a＜20），且它是3阶奇异长方形，请画出长方形ABCD及裁剪线的示意图，并在图的下方写出a的值．
（3）归纳与拓展：
已知长方形ABCD两邻边的长分别为b，c（b＜c），且它是4阶奇异长方形，求b：c（请画出长方形ABCD并在图下标出b：c的比值）
一个角的补角比它的余角的3倍少10°，则这个角是（　　）
A、80°B、48°
C、84°D、40°
已知：如图，在△ABC中，点D、E分别在边AB、AC上，且∠ABE=∠ACD，BE、CD交于点G．
（1）求证：△AED∽△ABC；
（2）如果BE平分∠ABC，求证：DE=CE．
电力部门统计，每天8：00点至21：00点是用电高峰期，21：00点至次日8：00是用电低谷期，为了缓解供电需求紧张的矛盾，电力部门采取更换分时电表的办法，换表前每度0.55元，换表后高峰期每度0.60元，低谷期每度0.40元．经过计算，小王家换表后使用了100度电，比换表前使用100度电节约了3元．问小王家高峰期和低谷期各用电多少度？
在平面直角坐标系中，直线l1的解析式为y=2x+3，直线l2过原点且l2与直线l1交于点P（-2，a）．
（1）求直线l2的解析式并在平面直角坐标系中画出直线l1和l2；
（2）设直线l1与x轴交于点A，试求△APO的面积．
（3）直线l1沿x轴的方向经过怎样的平移，就经过点B（1，-2）
（4）设直线l1与y轴交于点C，求点C到直线l2的距离．
下列图形中既是中心对称图形，又是轴对称图形的是（　　）
A、等边三角形B、等腰三角形
C、平行四边形D、线段

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网