题目内容
11.九年级三班学生苏琪为帮助同桌万宇巩固“平面直角坐标系四个象限内及坐标轴上的点的坐标特点”这一基础知识,在三张完全相同且不透明的卡片正面分别写上了-3,0,2三个数字,背面向上洗匀后随机抽取一张,将卡片上的数字记为a,再从剩下的两张中随机取出一张,将卡片上的数字记为b,然后叫万宇在平面直角坐标系中找出点M(a,b)的位置.(1)请你用树状图帮万宇同学进行分析,并写出点M所有可能的坐标;
(2)求点M在第二象限的概率;
(3)张老师在万宇同学所画的平面直角坐标系中,画了一个半径为3的⊙O,过点M能作多少条⊙O的切线?请直接写出答案.
分析 (1)画树状图展示所有6种等可能的结果数;
(2)根据第二象限点的坐标特征找出点M在第二象限的结果数,然后根据概率公式求解;
(3)画出图形得到在⊙O上的有2个点,在⊙O外的有2个点,在⊙O内的有2个点,则利用切线的定义可得过⊙O上的有2个点分别画一条切线,过⊙O外的有2个点分别画2条切线,但其中有2组切线重合,于是可判断过点M能作4条⊙O的切线.
解答 解:(1)画树状图为

共有6种等可能的结果数,它们是(-3,0)、(-3,2)、(0,-3)、(0,2)、(2,-3)、(2,0);
(2)只有(-3,2)在第二象限,
∴点M在第二象限的概率=$\frac{1}{6}$;
(3)如图,过点M能作4条⊙O的切线.
点评 本题考查了列表法与树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.利用切线的定义可解决(3)小题,应用数形结合的思想是解决此类题目的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.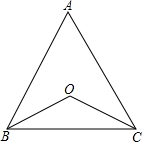 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
6.下列命题为真命题的是( )
| A. | 有两边及一角对应相等的两个三角形全等 | |
| B. | 方程x2-x+2=0有两个不相等的实数根 | |
| C. | 面积之比为1:4的两个相似三角形的周长之比是1:4 | |
| D. | 顺次连接任意四边形各边中点得到的四边形是平行四边形 |
16.某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
下列说法正确的是( )
| 成绩(分) | 46 | 47 | 48 | 49 | 50 |
| 人数(人) | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名同学的体育成绩的众数为50 | |
| B. | 这10名同学的体育成绩的中位数为48 | |
| C. | 这10名同学的体育成绩的方差为50 | |
| D. | 这10名同学的体育成绩的平均数为48 |
13.(-3)2+(-2)3=( )
| A. | -12 | B. | -17 | C. | 1 | D. | 17 |
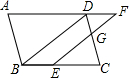 如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.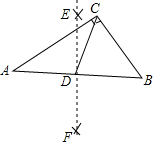 如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.
如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是5.