题目内容
1.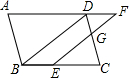 如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.(1)求证:BD∥EF;
(2)若$\frac{DG}{GC}$=$\frac{2}{3}$,BE=4,求EC的长.
分析 (1)根据平行四边的判定与性质,可得答案;
(2)根据相似三角形的判定与性质,可得答案.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
∵DF=BE,
∴四边形BEFD是平行四边形,
∴BD∥EF;
(2)∵四边形BEFD是平行四边形,
∴DF=BE=4.
∵DF∥EC,
∴△DFG∽CEG,
∴$\frac{DG}{CG}$=$\frac{DF}{CE}$,
∴CE=$\frac{DF•CG}{DG}$=4×$\frac{3}{2}$=6.
点评 本题考查了相似三角形的判定与性质,利用了平行四边形的判定与性质,相似三角形的判定与性质.

练习册系列答案
相关题目
16.五一期间刚到深圳的小明在哥哥的陪伴下,打算上午从莲山春早、侨城锦绣、深南溢彩中随机选择一个景点,下午从梧桐烟云、梅沙踏浪、一街两制中随机选择一个景点,小明恰好上午选中莲山春早,下午选中梅沙踏浪的概率是( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{9}$ | D. | $\frac{2}{9}$ |
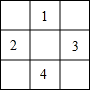 如图,将一块正方形地面等分成9块,其中标有1、2、3、4四个小方格是空地,另外五个小方格是草坪,一只自由飞行的小乌,随意地落在方格地面上,则小鸟落在草坪上的概率是$\frac{5}{9}$.
如图,将一块正方形地面等分成9块,其中标有1、2、3、4四个小方格是空地,另外五个小方格是草坪,一只自由飞行的小乌,随意地落在方格地面上,则小鸟落在草坪上的概率是$\frac{5}{9}$. 如图,AB∥CE,BF交CE于点D,DE=DF,∠F=20°,则∠B的度数为40°.
如图,AB∥CE,BF交CE于点D,DE=DF,∠F=20°,则∠B的度数为40°.