题目内容
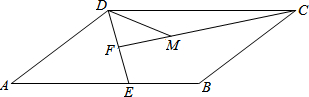 如图,平行四边形ABCD中,点E为AB边上一点,连接DE,点F为DE的中点,且CF⊥DE,点M为线段CF上一点,使DM=BE,∠DCM=
如图,平行四边形ABCD中,点E为AB边上一点,连接DE,点F为DE的中点,且CF⊥DE,点M为线段CF上一点,使DM=BE,∠DCM=| 1 |
| 3 |
(1)若AB=13,DE=10,求CF的长度;
(2)求证:CM=BC.
考点:平行四边形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)根据平行四边形的对边相等得出CD=AB=13,由F为DE中点,得出DF=
DE=5,然后在直角△DCF中利用勾股定理即可求出CF的长度;
(2)连接CE,根据∠DCM=
∠DMF,推出∠CDM=2∠DCM,根据CF⊥DE,F为DE中点,推出CD=CE,∠CDF=∠CEF,根据平行线的性质得出∠CDF+∠BEF=180°,进而推出推出∠CEB=2∠DCM,从而证得∠CDM=∠CEB,即可证得△CDM≌△CEB,推出CM=BC.
| 1 |
| 2 |
(2)连接CE,根据∠DCM=
| 1 |
| 3 |
解答:解:(1)∵四边形ABCD是平行四边形,
∴CD=AB=13,
∵F为DE中点,
∴DF=
DE=5,
∵CF⊥DE,
∴CF=
=
=12;
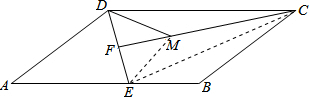 (2)连接CE,
(2)连接CE,
∵∠DCM=
∠DMF.
∴∠DMF=∠CDM+∠DCF=3∠DCM,
∴∠CDM=2∠DCM,
∵AB∥CD,
∴∠CDF+∠BEF=180°,
∴∠CDF+∠CEF+∠CEB=180°
∵CF⊥DE,F为DE中点,
∴CD=CE,∠CDF=∠CEF,
∴2∠CDF+∠CEB=180°,
∵∠CDF=90°-∠DCM,
∴∠CEB=2∠DCM,
∴∠CDM=∠CEB
在△CDM和△CEB中,
,
∴△CDM≌△CEB(SAS),
∴CM=BC.
∴CD=AB=13,
∵F为DE中点,
∴DF=
| 1 |
| 2 |
∵CF⊥DE,
∴CF=
| CD2-DF2 |
| 132-52 |
 (2)连接CE,
(2)连接CE,∵∠DCM=
| 1 |
| 3 |
∴∠DMF=∠CDM+∠DCF=3∠DCM,
∴∠CDM=2∠DCM,
∵AB∥CD,
∴∠CDF+∠BEF=180°,
∴∠CDF+∠CEF+∠CEB=180°
∵CF⊥DE,F为DE中点,
∴CD=CE,∠CDF=∠CEF,
∴2∠CDF+∠CEB=180°,
∵∠CDF=90°-∠DCM,
∴∠CEB=2∠DCM,
∴∠CDM=∠CEB
在△CDM和△CEB中,
|
∴△CDM≌△CEB(SAS),
∴CM=BC.
点评:本题考查了平行四边形的性质,全等三角形的性质和判定,三角形外角的性质,直角三角形的性质,全等三角形的性质和判定的应用,主要考查学生的推理能力.

练习册系列答案
相关题目
 如图,在△ABC中,∠C=Rt∠,以顶点C为圆心,BC为半径作圆.若AC=4,tanA=
如图,在△ABC中,∠C=Rt∠,以顶点C为圆心,BC为半径作圆.若AC=4,tanA=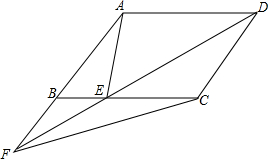 如图,E为平行四边形ABCD的边BC上的一个动点,延长DE交AB的延长线于F,连结AE、AF,
如图,E为平行四边形ABCD的边BC上的一个动点,延长DE交AB的延长线于F,连结AE、AF,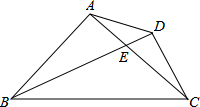 如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,若点D为△ABC外一点,且∠ADC=135°,判断BD和CD的位置关系.
如图,等腰Rt△ABC中,AB=AC,∠BAC=90°,BE平分∠ABC交AC于E,若点D为△ABC外一点,且∠ADC=135°,判断BD和CD的位置关系.