题目内容
已知函数y=x2-(m2+4)x-2m2-12.
(1)当m取何值时,此函数有最小值-
,求出此时x的值;
(2)求证:不论m取任何实数,抛物线都过一定点,并求出定点坐标.
(1)当m取何值时,此函数有最小值-
| 81 |
| 4 |
(2)求证:不论m取任何实数,抛物线都过一定点,并求出定点坐标.
考点:二次函数的最值,二次函数图象上点的坐标特征
专题:
分析:(1)根据函数顶点的纵坐标是函数的最小值,可得关于m的方程,根据解方程,可得m的值,根据函数顶点的坐标公式,可得函数定点的横坐标;
(2)根据因式分解,可得交点式函数解析式,根据交点坐标,可得答案.
(2)根据因式分解,可得交点式函数解析式,根据交点坐标,可得答案.
解答:(1)解:y最小=
=
=-
,
m4+16m2-17=0
(m2-1)(m2+17)=0
∵m2+17≠0,
∴m=±1,
∴y=x2-5x-14
x=-
=-
=
,
当m=±1时,此函数有最小值-
,此时x=
;
(2)证明:∵此函数可以写成y=(x+2)•[x-(m2+6)],
∴函数与x轴的交点为(-2,0),(m2+6,0),
∴不论m取任何实数,抛物线都过一定点,定点坐标是(-2,0).
| 4ac-b2 |
| 4a |
| 4(-2m2-12)-[-(m2+4)]2 |
| 4 |
| 81 |
| 4 |
m4+16m2-17=0
(m2-1)(m2+17)=0
∵m2+17≠0,
∴m=±1,
∴y=x2-5x-14
x=-
| b |
| 2a |
| -5 |
| 2 |
| 5 |
| 2 |
当m=±1时,此函数有最小值-
| 81 |
| 4 |
| 5 |
| 2 |
(2)证明:∵此函数可以写成y=(x+2)•[x-(m2+6)],
∴函数与x轴的交点为(-2,0),(m2+6,0),
∴不论m取任何实数,抛物线都过一定点,定点坐标是(-2,0).
点评:本题考查了函数的最值,利用了函数的顶点的纵坐标是函数的最小值.

练习册系列答案
相关题目
某班男生比女生多
,男生相当于全班人数的( )
| 3 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
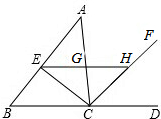 已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EH∥BC,分别交AC、CF于点G、H.求证:GE=GH.
已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EH∥BC,分别交AC、CF于点G、H.求证:GE=GH. 小华用透明的纸糊的四边形风筝.糊好后用手边的量角器测量发现,无论支架AB与CD有多长,只要满足DA=DB,CA=CB,∠CAD与∠CBD总是相等的,为什么?
小华用透明的纸糊的四边形风筝.糊好后用手边的量角器测量发现,无论支架AB与CD有多长,只要满足DA=DB,CA=CB,∠CAD与∠CBD总是相等的,为什么?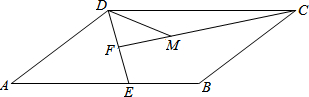 如图,平行四边形ABCD中,点E为AB边上一点,连接DE,点F为DE的中点,且CF⊥DE,点M为线段CF上一点,使DM=BE,∠DCM=
如图,平行四边形ABCD中,点E为AB边上一点,连接DE,点F为DE的中点,且CF⊥DE,点M为线段CF上一点,使DM=BE,∠DCM=