题目内容
如图，在△ABC中，∠C=Rt∠，以顶点C为圆心，BC为半径作圆．若AC=4，tanA=| 3 |
| 4 |
（1）求AB长；
（2）求⊙C截AB所得弦BD的长．
考点：垂径定理,勾股定理,解直角三角形
专题：
分析：（1）利用锐角三角函数关系得出BC的长，再利用勾股定理求出AB的长；
（2）利用等积法得出EC的长，再利用勾股定理求出即可．
（2）利用等积法得出EC的长，再利用勾股定理求出即可．
解答：
解：（1）∵AC=4，tanA=
=
，
∴BC=3；
∴在Rt△CB中，AB=
=5；
（2）过点C作AB垂线，垂足为E，
∵CE×AB=AC×BC，
∴CE=
，
∵BE=
=
=
，
∴BD=2BE=
．
解：（1）∵AC=4，tanA=| BC |
| AC |
| 3 |
| 4 |
∴BC=3；
∴在Rt△CB中，AB=
| AC2+BC2 |
（2）过点C作AB垂线，垂足为E，
∵CE×AB=AC×BC，
∴CE=
| 12 |
| 5 |
∵BE=
| BC2-CE2 |
32-(
|
| 9 |
| 5 |
∴BD=2BE=
| 18 |
| 5 |
点评：此题主要考查了垂径定理以及勾股定理，得出CE的长是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
小华用透明的纸糊的四边形风筝．糊好后用手边的量角器测量发现，无论支架AB与CD有多长，只要满足DA=DB，CA=CB，∠CAD与∠CBD总是相等的，为什么？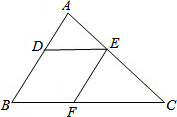
如图，在△ABC中，D、E、F分别是AB、AC、BC上的点，且DE∥BC，EF∥AB，AD：DB=2：3，BC=20cm，求BF的长．
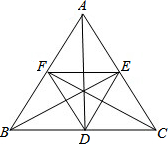已知：如图，AB、BE、CF是等边△ABC的角平分线．求证：△DEF是等边三角形．
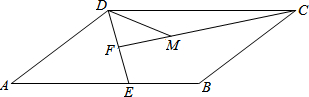如图，平行四边形ABCD中，点E为AB边上一点，连接DE，点F为DE的中点，且CF⊥DE，点M为线段CF上一点，使DM=BE，∠DCM=
如图，⊙O是△ABC的外接圆，AD平分∠BAC，交⊙O于点D，弦DE∥BA，交AC于点F，OF与AD有怎样的位置关系，为什么？