题目内容
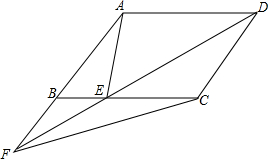如图，E为平行四边形ABCD的边BC上的一个动点，延长DE交AB的延长线于F，连结AE、AF，（1）△ABE与△CEF的面积有何关系？请证明你的猜想；
（2）若E在BC的延长线上，（1）中的结论还成立吗？请给出你的理由．
考点：平行四边形的性质
专题：
分析：（1）根据四边形ABCD是平行四边形，点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，得出S△CBF=S△DBF，所以S△CBF-S△EBF=S△DBF-S△EBF，得出S△DBE=S△CEF，根据△ABE和△DBE同底等高，则S△ABE=S△DBE，即可证得．
（2）根据四边形ABCD是平行四边形，点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，得出S△CBF=S△DBF，所以S△EBF-S△CBF=S△EBF-S△DBF，得出S△DBE=S△CEF，根据△ABE和△DBE同底等高，则S△ABE=S△DBE，即可证得．
（2）根据四边形ABCD是平行四边形，点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，得出S△CBF=S△DBF，所以S△EBF-S△CBF=S△EBF-S△DBF，得出S△DBE=S△CEF，根据△ABE和△DBE同底等高，则S△ABE=S△DBE，即可证得．
解答：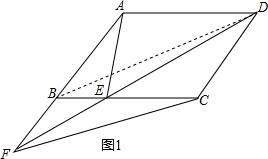
解：（1））△ABE与△CEF的面积相等；
理由：如图1，连接BD，
∵四边形ABCD是平行四边形，
∴点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，
∴S△CBF=S△DBF，
∴S△CBF-S△EBF=S△DBF-S△EBF，
∴S△DBE=S△CEF，
∵△ABE和△DBE同底等高，S△ABE=S△DBE，
∴S△ABE=S△CEF．
（2）成立；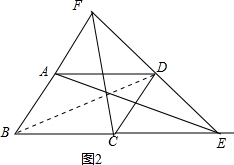
如图2，连接BD，
∵四边形ABCD是平行四边形，
∴点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，
∴S△CBF=S△DBF，
∴S△EBF-S△CBF=S△EBF-S△DBF，
∴S△CEF=S△DBE，
∵△ABE和△DBE同底等高，S△ABE=S△DBE，
∴S△ABE=S△CEF．
解：（1））△ABE与△CEF的面积相等；理由：如图1，连接BD，
∵四边形ABCD是平行四边形，
∴点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，
∴S△CBF=S△DBF，
∴S△CBF-S△EBF=S△DBF-S△EBF，
∴S△DBE=S△CEF，
∵△ABE和△DBE同底等高，S△ABE=S△DBE，
∴S△ABE=S△CEF．
（2）成立；
如图2，连接BD，
∵四边形ABCD是平行四边形，
∴点D和点C到AB边的距离是相等的 即△CBF和△DBF的BF边上高相等，
∴S△CBF=S△DBF，
∴S△EBF-S△CBF=S△EBF-S△DBF，
∴S△CEF=S△DBE，
∵△ABE和△DBE同底等高，S△ABE=S△DBE，
∴S△ABE=S△CEF．
点评：本题考查了平行四边形的性质，三角形的面积，根据同底等高找出面积相等的三角形是本题的关键．
练习册系列答案
相关题目
某班男生比女生多
，男生相当于全班人数的（ ）
| 3 |
| 8 |
A、
| ||
B、
| ||
C、
| ||
D、
|
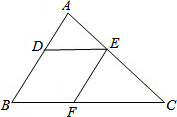如图，在△ABC中，D、E、F分别是AB、AC、BC上的点，且DE∥BC，EF∥AB，AD：DB=2：3，BC=20cm，求BF的长．
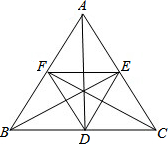已知：如图，AB、BE、CF是等边△ABC的角平分线．求证：△DEF是等边三角形．
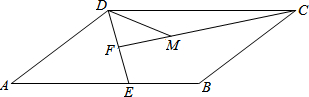如图，平行四边形ABCD中，点E为AB边上一点，连接DE，点F为DE的中点，且CF⊥DE，点M为线段CF上一点，使DM=BE，∠DCM=
如图，将一副三角尺如图所示叠放在一起，若AB=12cm，则阴影部分的面积是（ ）| A、12 | B、18 | C、24 | D、36 |
已知AD是△ABC的高，△ABC外接圆的半径为R，