题目内容
在△ABC中,∠BAC=90°,AD是BC边上的高,∠ABC的角平分线交AD于E,EF∥BC,交AC于点F,你能猜想出线段AE与CF的数量关系吗?请说明理由.
考点:平行四边形的判定与性质
专题:
分析:延长FE交AB于G.作GH∥AC交BC于H.连接EH,得出四边形FGHC为平行四边形,得出GH=CF.∠FCD=∠EGH,进而求得∠HGF=∠BAD,得出∠BGH=90°,根据,∠ABC的角平分线交AD于E,EF∥BC,得出GE=GB,∠AGE=∠ABD,最后通过△AGE≌△DBG求得结论.
解答:解:AE=CF,
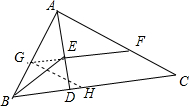 理由:延长FE交AB于G.作GH∥AC交BC于H.连接EH,
理由:延长FE交AB于G.作GH∥AC交BC于H.连接EH,
∵EF∥BC,
∴FG∥BC.
∴四边形FGHC为平行四边形,
∴GH=CF.∠FCD=∠EGH,
∵∠BAC=90°,AD是BC边上的高,
∴∠ACB=∠BAD,
∴∠EGH=∠BAD,
∵FG∥BC.AD⊥BC,
∴∠AEG=90°,
∴∠BAD+∠AGE=90°,
∴∠EGH+∠AGE=90°,
即∠AGH=90°,
∵GF∥BC,
∴∠GED=∠EBD,∠AGE=∠ABD,
∵∠GBE=∠EBD,
∴∠GBE=∠GEB,
∴GE=GB,
在△AGE和△DBG中
∴△AGE≌△DBG(AAS),
∴GH=AE,
∴AE=CF.
 理由:延长FE交AB于G.作GH∥AC交BC于H.连接EH,
理由:延长FE交AB于G.作GH∥AC交BC于H.连接EH,∵EF∥BC,
∴FG∥BC.
∴四边形FGHC为平行四边形,
∴GH=CF.∠FCD=∠EGH,
∵∠BAC=90°,AD是BC边上的高,
∴∠ACB=∠BAD,
∴∠EGH=∠BAD,
∵FG∥BC.AD⊥BC,
∴∠AEG=90°,
∴∠BAD+∠AGE=90°,
∴∠EGH+∠AGE=90°,
即∠AGH=90°,
∵GF∥BC,
∴∠GED=∠EBD,∠AGE=∠ABD,
∵∠GBE=∠EBD,
∴∠GBE=∠GEB,
∴GE=GB,
在△AGE和△DBG中
|
∴△AGE≌△DBG(AAS),
∴GH=AE,
∴AE=CF.
点评:本题考查了平行线的性质,角平分线的性质,等腰三角形的判定,平行四边形的判定和性质,三角形全等的判定和性质,作出辅助线构建平行四边形是本题的关键.

练习册系列答案
相关题目
下列图形中,∠1与∠2是对顶角的是( )
A、 |
B、 |
C、 |
D、 |
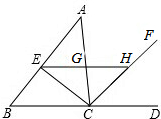 已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EH∥BC,分别交AC、CF于点G、H.求证:GE=GH.
已知:如图,∠ACD是△ABC的一个外角,CE、CF分别平分∠ACB、∠ACD,EH∥BC,分别交AC、CF于点G、H.求证:GE=GH.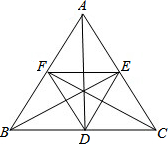 已知:如图,AB、BE、CF是等边△ABC的角平分线.求证:△DEF是等边三角形.
已知:如图,AB、BE、CF是等边△ABC的角平分线.求证:△DEF是等边三角形.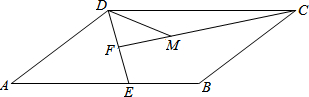 如图,平行四边形ABCD中,点E为AB边上一点,连接DE,点F为DE的中点,且CF⊥DE,点M为线段CF上一点,使DM=BE,∠DCM=
如图,平行四边形ABCD中,点E为AB边上一点,连接DE,点F为DE的中点,且CF⊥DE,点M为线段CF上一点,使DM=BE,∠DCM=