题目内容
14.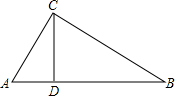 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2}{3}$ |
分析 在直角△ABC中,根据勾股定理即可求得AB,而∠B=∠ACD,即可把求sin∠ACD转化为求sinB.
解答 解:在直角△ABC中,根据勾股定理可得:AB2=AC2+BC2,
∴AB=$\sqrt{5+4}$=3.
∵∠B+∠BCD=90°,∠ACD+∠BCD=90°,
∴∠B=∠ACD.
∴sin∠ACD=sin∠B=AC:AB=$\frac{2}{3}$,
故选D.
点评 本题考查了解直角三角形中三角函数的应用,要熟练掌握好边角之间的关系,难度适中.

练习册系列答案
相关题目
9.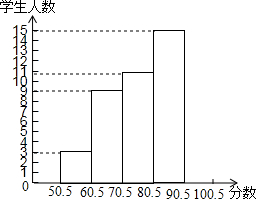 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
(1)根据以上信息,统计表中A=0.18,B=12,C=0.24;
(2)补全统计图;
(3)在该问题中,个体是每一个学生的竞赛成绩;
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
 为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.
为了了解奥运知识,某中学举行了一次“奥运知识竞赛”,共有900名学生参加了这次竞赛,为了了解本次竞赛情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分),进行统计,请你根据下面尚未完成的统计表和统计图,解答下列问题.| 分组 | 频数 | 频率 |
| 50.5~60.5 | 3 | 0.06 |
| 60.5~70.5 | 9 | A |
| 70.5~80.5 | 11 | 0.22 |
| 80.5~90.5 | 15 | 0.30 |
| 90.5~100.5 | B | C |
(2)补全统计图;
(3)在该问题中,个体是每一个学生的竞赛成绩;
(4)若成绩在90分以上(不含90分)为优秀,则该校成绩优秀的约为多少人?
19.已知一元二次方程ax2+bx+c=0的一个根是x1=0,二次函数y=ax2+bx+c关于直线x=1对称,则方程的另一根为( )
| A. | x2=0 | B. | x2=1 | C. | x2=-2 | D. | x2=2 |
4.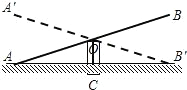 如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
 如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )
如图,是跷跷板的示意图,支柱OC与地面垂直,O是AB的中点,若∠OAC=20°,当跷跷板绕O转到A′B′位置时,∠AOA′的大小是( )| A. | 40° | B. | 60° | C. | 80° | D. | 20° |
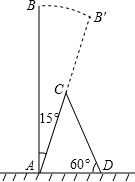 一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)
一棵大树树干AB(假定树干AB垂直于地面)被刮倾斜15°后折断在地上,树的项部恰好接触到地面D(如图所示),量得树干的倾斜角为∠BAC=15°,大树被折断部分和地面所成的角∠ADC=60°,AD=3.6米,求这棵大树AB原来的高度是多少米?(参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7,$\sqrt{6}$≈2.4)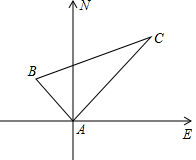 甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.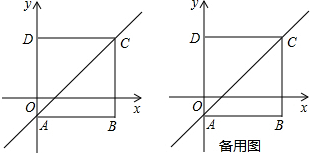
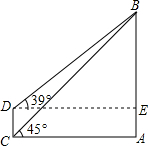 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)