题目内容
19.已知一元二次方程ax2+bx+c=0的一个根是x1=0,二次函数y=ax2+bx+c关于直线x=1对称,则方程的另一根为( )| A. | x2=0 | B. | x2=1 | C. | x2=-2 | D. | x2=2 |
分析 关于x的一元二次方程ax2+bx+c=0(a≠0)的根即为二次函数y=ax2+bx+c(a≠0)的图象与x轴的交点.
解答 解:∵一元二次方程ax2+bx+c=0的一个根是x1=0,
∴抛物线y=ax2+bx+c(a≠0)与x轴的一个交点是(0,0),
∵对称轴是x=1.
设该抛物线与x轴的另一个交点是(x,0).则$\frac{x+0}{2}$=1,
解得,x=2,
即该抛物线与x轴的另一个交点是(2,0).
所以关于x的一元二次方程ax2+bx+c=0(a≠0)的另一个根为x=2.
故选:D.
点评 本题考查了抛物线与x轴的交点.解题时,注意抛物线y=ax2+bx+c(a≠0)与关于x的一元二次方程ax2+bx+c=0(a≠0)间的转换.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.若点(-1,2)在反比例函数y=$\frac{k}{x}$的图象上,则下列各点一定在该图象上的是( )
| A. | (-2,-1) | B. | (-$\frac{1}{2}$,2) | C. | (2,-1) | D. | ($\frac{1}{2}$,2) |
14.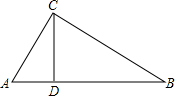 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2}{3}$ |
4.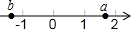 已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
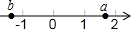 已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )
已知a,b两数在数轴上对应的点的位置如图所示,则化简代数式|a+b|-|a-2|+|b+2|的结果是( )| A. | 2a+2b | B. | 2b+3 | C. | 2a-3 | D. | -1 |
11. 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠3 | D. | ∠3+∠4=180° |
9.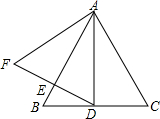 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
 如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )
如图,等腰三角形ABC中,AB=AC,∠BAC=70°,D是BC中点,DE⊥AB于E,延长DE至F,使EF=DE,则∠F的度数是( )| A. | 30° | B. | 35° | C. | 55° | D. | 60° |
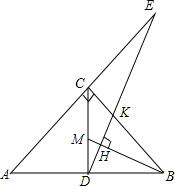 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证: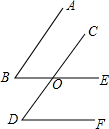 已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF.
已知:如图,AB∥CD,∠B=∠D,求证:BE∥DF.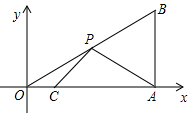 如图,已知A(3,0)、B(3,$\sqrt{3}$)、C(1,0),点P为OB上的一动点,则PA+PC的最小值为$\sqrt{7}$.
如图,已知A(3,0)、B(3,$\sqrt{3}$)、C(1,0),点P为OB上的一动点,则PA+PC的最小值为$\sqrt{7}$.