题目内容
6.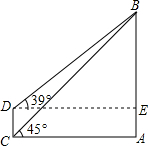 目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)
目前世界上最高的电视塔是广州新电视塔.如图所示,新电视塔高AB为610米,远处有一栋大楼,某人在楼底C处测得塔顶B的仰角为45°,在楼顶D处测得塔顶B的仰角为39°,(sin39°≈0.63,cos39°≈0.78,tan39°≈0.81)(1)求大楼与电视塔之间的距离AC;
(2)求大楼的高度CD(精确到1米)
分析 (1)判断出△BAC为等腰直角三角形,即可求出AC的长;
(2)在Rt△DEB中,根据$\frac{BE}{DE}$=tan39°即可求出CD的长.
解答 解:(1)∵塔顶B的仰角为45°,
∴∠ABC=∠ACB=45°,
∴AC=AB=610米;
(2)根据题意可知四边形ACDE为矩形,
则AC=DE,设AE=DC=x米,
则BE=(610-x)米,
在Rt△DEB中,$\frac{BE}{DE}$=tan39°,
∴$\frac{610-x}{610}$≈0.81,
解得x≈116.
答:大楼与电视塔之间的距离AC为610米,大楼的高CD为116米.
点评 本题考查了解直角三角形的应用---仰角俯角问题,熟悉等腰三角形的性质和三角函数的定义是解题的关键.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
14.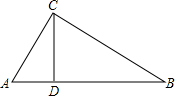 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2}{3}$ |
11. 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )
 如图,能判断直线AB∥CD的条件是( )
如图,能判断直线AB∥CD的条件是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠1=∠3 | D. | ∠3+∠4=180° |
15.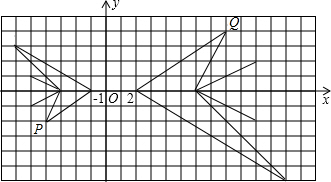 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )| A. | (-2a,-2b) | B. | (-a,-2b) | C. | (-2b,-2a) | D. | (-2a,-b) |




 已知:AB∥CD,EF∥CD,且∠ABC=20°,∠CFE=30°,则∠BCF的度数是50°.
已知:AB∥CD,EF∥CD,且∠ABC=20°,∠CFE=30°,则∠BCF的度数是50°. 已知:如图,AB⊥BD,AD⊥AB,∠D=100°,AC平分∠BCD,求∠DAC的度数.
已知:如图,AB⊥BD,AD⊥AB,∠D=100°,AC平分∠BCD,求∠DAC的度数.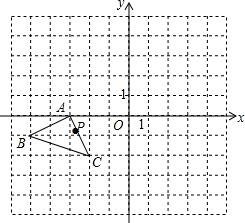 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移得到△A1B1C1,且点P的对应点为P1(a+5,b+4).