题目内容
5.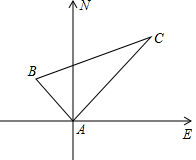 甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
甲乙两轮船同时从港口A开出,其中甲轮船每小时航行12海里,乙轮船每小时航行16海里,它们离开港口一个半小时后分别位于B,C两处,且相距30海里,如果甲轮船的航行方向为北偏西40°,请你确定乙轮船的航行方向.
分析 根据题意得到BC、AB、AC,然后根据勾股定理逆定理判断出∠BAC的度数,解答即可.
解答 解:由题意可知:
BC=30,
AB=12×1.5=18,
AC=16×15=24,
BC2=302=900,
AB2+AC2=182+242=900,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∴∠YAC=90°-40°=50°.
答:乙轮船航行方向为北偏东50°方向.
点评 本题考查了解直角三角形的应用---方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合,体现了数学应用于实际生活的思想.

练习册系列答案
相关题目
13. 如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
 如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )
如图,矩形ABCD中,AB=2,BC=3,点P是BC边上任意一点,E,F,R分别是AP,RP,CD的中点,则EF的长为( )| A. | $\frac{\sqrt{13}}{2}$ | B. | $\frac{\sqrt{10}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
14.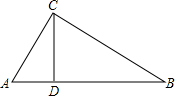 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,若BC=$\sqrt{5}$,AC=2,则sin∠ACD的值为( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | $\frac{2}{3}$ |
15.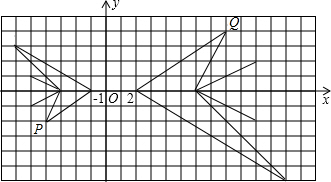 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
 某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )
某学习小组在讨论“变化的鱼”,已知如图中的大鱼与小鱼是以原点O为位似中心的位似图形,且大鱼与小鱼的位似比是2:1,若小鱼上的点P(a,b),对应大鱼上的点Q,则点Q的坐标为( )| A. | (-2a,-2b) | B. | (-a,-2b) | C. | (-2b,-2a) | D. | (-2a,-b) |
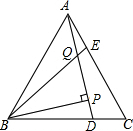 如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.
如图,已知在等边△ABC中,D、E是BC,AC上的点,AE=CD,AD与BE相交于Q,BP丄AD,则$\frac{PQ}{BQ}$的值是$\frac{1}{2}$.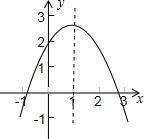 已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,下列说法①a>0;②b2-4ac>0;③4a+2b+c>0;④c<0;⑤b>0.其中正确的有( )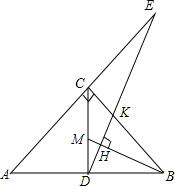 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,M是CD上的点,DH⊥BM于H,DH的延长线交AC的延长线于E.求证:


